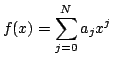 とおく.
ここで各aj は整数である.
とおく.
ここで各aj は整数である.
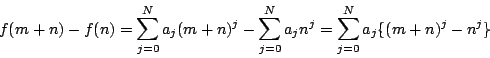
ここで,
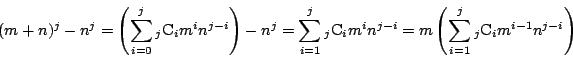
である.ゆえに f(m+n)-f(n) は m の倍数である.
f(n+f(n)k)-f(n)=M(k)f(n)
つまり
と表せる. 任意の自然数 n に対し f(n) が素数なので f(n+f(n)k) も素数. f(n)=1 となる n が無数にあれば恒等式の原理から f(x) は定数. f(n)=0 となる n が無数にあれば恒等式の原理から f(x) は定数. f(n) が0でも1でもない n が存在するとき,その n を固定する. このときすべての k に対して
f(n+f(n)k)=f(n)
がすべての k について成立.