次: 慶応理工 上: 解答 前: 横国大後期理系

京都府立医大

(1)

$$F(x)=Ax^4+ax^3+bx^2+cx+d$$ を実数を係数とする4次式とする． F(x)=0 の解を $\alpha$ とする． $\alpha$ が虚数の場合， $\overline{\alpha}$ で $\alpha$ の共役複素数を表すと， $F(\alpha)=0$ より，

$$\begin{eqnarray*}\overline{F(\alpha)}&=&\overline{A\alpha^4+a\alpha^3+b\alpha^2+... ...\alpha})^2+c(\overline{\alpha})+d\\ &=&F(\overline{\alpha})=0 \end{eqnarray*}$$

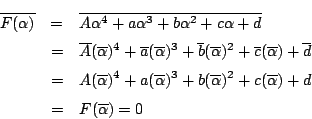
したがって， $\overline{\alpha}$ もまたF(x)=0 の解である． さて因数定理によって F(x) は

$$F(x)=(x-\alpha)Q(x)$$

と因数分解され， Q(x) は3次式である．Q(x)=0の解を $\beta$ とする．再び

$$Q(x)=(x-\beta)Q_2(x) \quad つまり\ F(x)=(x-\alpha)(x-\beta)Q_2(x)$$

これをくり返せば， F(x) は1次式4つと定数の積になる． x⁴ の係数比較から

$$F(x)=A(x-\alpha)(x-\beta)(x-\gamma)(x-\delta)$$

と表される． $\alpha,\ \beta,\ \gamma,\ \delta$ が実数なら $A(x-\alpha)(x-\beta)$ ， $(x-\gamma)(x-\delta)$ はそれぞれ実数係数の2次式なので成立． $\alpha$ が虚数のとき，上に見たように $\beta,\ \gamma,\ \delta$のいずれかは $\overline{\alpha}$ である．これを $\beta$ とする．このとき

$$(x-\alpha)(x-\overline{\alpha}) =x^2-(\alpha+\overline{\alpha})x+\alpha\overline{\alpha}$$

より， $A(x-\alpha)(x-\overline{\alpha})$は実数係数の2次式である． $(x-\gamma)(x-\delta)$は $\gamma,\ \delta$ がともに実数か，たがいに共役な虚数なので やはり実数係数の2次式である． よって実数を係数とする任意の4次式は実数を係数とする2つの2次式の 積であることが示された．

(2)

(1)から f(x) は実数を係数とする2つの2次式の積に分解される．それを

f(x)=(lx²+mx+n)(sx²+tx+u)

とする． ls=1 なので

(lx²+mx+n)(sx²+tx+u)=(lsx²+msx+ns)(slx²+tlx+ul)=(x²+msx+ns)(x²+tlx+ul)

となる．よってはじめから x² の係数が1の2つの2次式 $h(x),\ k(x)$ で

f(x)=h(x)k(x)

と分解されるとしてよい． 十分大きな2つの実数 $v,\ w$ を適当にとると

$$h(x)-v=0,\ k(x)-w=0$$

がともに相異なる2つずつの解をもつようにできる．つまり

(h(x)-v)(k(x)-w)=0

は相異なる4つの実数解をもつ．この等式は

h(x)k(x)=vk(x)+wh(x)-vw

と変形される．したがって

g(x)=vk(x)+wh(x)-vw

とおけば，確かに g(x)=vk(x)+wh(x)-vwは実数係数の2次式で， 4次方程式 f(x)=g(x) は4つの相異なる実数解をもつ．