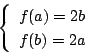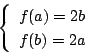次: 慶応医
上: 問題
前: 名大前期文系
正の整数 a に対し, a の正の約数全体の和を f(a) で表す.
ただし,1および a 自身も約数とする.たとえば f(1)=1であり,
a=15 ならば15の正の約数は1,3,5,15なのでf(15)=24となる.次の問いに答えよ.
-
- (1)
- a が正の奇数 b と正の整数 m を用いてa=2mbと表されるとする.
このとき
f(a)=(2m+l-1)f(b)
が成り立つことを示せ.
- (2)
- a が2以上の整数 p と正の整数 q を用いてa=pqと表されるとする.
このとき
が成りたつことを示せ.また,等号が成り立つのは,q=1かつpが素数であるときに
限ることを示せ.
- (3)
- 正の偶数
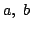 は,ある整数
は,ある整数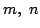 とある奇数
とある奇数 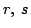 を用いて
を用いて
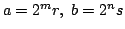 のように表すことができる.このとき
のように表すことができる.このとき 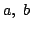 が
が
をみたせば,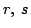 は素数であり,かつ
は素数であり,かつ
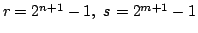 となることを示せ.
となることを示せ.
AozoraGakuen
2002-06-21