


次: 金沢前期理系
上: 問題
前: 九大前期理系
設問(1)から(5)に答えなさい.
4で割ると余りが1になるような素数
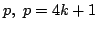 ,を1つとる.これに対し,等式
,を1つとる.これに対し,等式
を満たす自然数3つの組
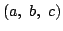 の全体を考える.両辺の絶対値を比べればわかるよう
に,このような自然数3つの組の可能性は有限通りしかありえない.
の全体を考える.両辺の絶対値を比べればわかるよう
に,このような自然数3つの組の可能性は有限通りしかありえない.
いま等式(Q)を満たす自然数3つの組
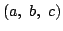 から新しく自然数3つの組を作る手続きを
次の(i),(ii),(iii)により定める:
から新しく自然数3つの組を作る手続きを
次の(i),(ii),(iii)により定める:
-
- (1)
- a<b-cならば
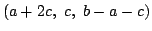 を作る;
を作る;
- (2)
- b-c<a<2bならば
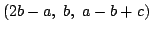 を作る;
を作る;
- (3)
- a>2bならば
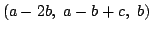 を作る.
を作る.
-
- (1)
-
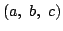 が等式(Q)を満たす自然数の組でさらに(i)の条件a<b-cを満
たすとする.このとき,上の(i)より得られる
が等式(Q)を満たす自然数の組でさらに(i)の条件a<b-cを満
たすとする.このとき,上の(i)より得られる
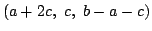 もまた等式
(Q)を満たすことを示しなさい.
もまた等式
(Q)を満たすことを示しなさい.
- (2)
- 等式(Q)を満たす自然数の組
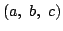 はa=b-cやa=2bを満たすことは
ないことを示しなさい.
はa=b-cやa=2bを満たすことは
ないことを示しなさい.
- (3)
- 等式(Q)を満たす自然数の組
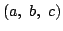 の中には,上の手続きを施しても変化し
ないという性質を持つものが存在する.p=4k+1と表すとき,この性質を持つ
の中には,上の手続きを施しても変化し
ないという性質を持つものが存在する.p=4k+1と表すとき,この性質を持つ
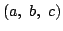 を k を用いて具体的に与え,かっそれがただ1組しか存在しないことを
示しなさい.
を k を用いて具体的に与え,かっそれがただ1組しか存在しないことを
示しなさい.
- (4)
- 等式(Q)を満たす自然数の組
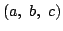 に対して上の手続きを2回繰返して施す
とどうなるか,結論を簡潔に説明しなさい.また,この観察をもとに等式(Q)を満たす自
然数3つの組の全体の個数が偶数か奇数かを決定し,そう判断できる理由を述べなさい.
ただし,等式(Q)を満たす自然数3つの細から上の手続きにより新しく作られた自然数3つの
組は(i),(ii),(iii)のどの場合でも再び等式(Q)を満たすという事実については
ここでは証明なしに用いてよい.
に対して上の手続きを2回繰返して施す
とどうなるか,結論を簡潔に説明しなさい.また,この観察をもとに等式(Q)を満たす自
然数3つの組の全体の個数が偶数か奇数かを決定し,そう判断できる理由を述べなさい.
ただし,等式(Q)を満たす自然数3つの細から上の手続きにより新しく作られた自然数3つの
組は(i),(ii),(iii)のどの場合でも再び等式(Q)を満たすという事実については
ここでは証明なしに用いてよい.
- (5)
- 素数p=4k+1をある2っの自然数
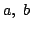 により
により
p=a2+(2b)2
と表すことができることを示しなさい.
AozoraGakuen
2002-06-21
![]() ,を1つとる.これに対し,等式
,を1つとる.これに対し,等式
![]() から新しく自然数3つの組を作る手続きを
次の(i),(ii),(iii)により定める:
から新しく自然数3つの組を作る手続きを
次の(i),(ii),(iii)により定める: