

 次: 2. 解答
上: 1. 問題
前: 4.
平面上に原点Oを中心とする半径1の円 C1と点
次: 2. 解答
上: 1. 問題
前: 4.
平面上に原点Oを中心とする半径1の円 C1と点
 を中心とする
半径1の円 C2がある.ただし
を中心とする
半径1の円 C2がある.ただし
 とする.円 C2と x 軸との交点を
とする.円 C2と x 軸との交点を
 とし,
とし,
 を通り
y 軸と平行な直線をそれぞれ
を通り
y 軸と平行な直線をそれぞれ 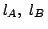 とする.2直線
とする.2直線 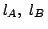 で
はさまれた領域の部分で,円 C1の外部で円 C2の内部であるものを D1 ,
円 C2の外部で円 C1の内部であるものを D2とする.いま,
で
はさまれた領域の部分で,円 C1の外部で円 C2の内部であるものを D1 ,
円 C2の外部で円 C1の内部であるものを D2とする.いま, 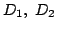 をそれぞれ
x 軸のまわりに1回転させてできる回転体の体積を
をそれぞれ
x 軸のまわりに1回転させてできる回転体の体積を
 とする.
とする.
-
- (1)
 ,
,
 をそれぞれ
をそれぞれ 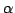 を用いて表せ.
を用いて表せ.
- (2)
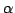 が
が
 の範囲を動くとき,
の範囲を動くとき,
 の最大値を求めよ.
の最大値を求めよ.
AozoraGakuen
2002-03-01
 の範囲を動くとき,
の範囲を動くとき,
 とする.円 C2と x 軸との交点を
とする.円 C2と x 軸との交点を
 の範囲を動くとき,
の範囲を動くとき,