京大特色4番
$xy$平面上の格子点とは,その点の$x$座標と$y$座標がともに整数となる点のことをいう.
$n$を2以上の整数とする.$xy$平面上で不等式
\[
0\leqq x \leqq n-1,\ \quad 0\leqq y,\ \quad \sqrt{5}y\leqq x
\]
で表される領域を$D_n$とする.$D_n$に属する格子点の個数を$S_n$とおく.
例えば,$n=5$のとき,$D_5$に属する格子点は
$(0,\ 0)$,
$(1,\ 0)$,
$(2,\ 0)$,
$(3,\ 0)$,
$(4,\ 0)$,
$(3,\ 1)$,
$(4,\ 1)$の7個であるから,$S_5=7$となる.
また$n=9$のときは,以下のように領域$D_9$に属する格子点は全部で21個存在するから,$S_9=21$である.
以下の設問に答えよ.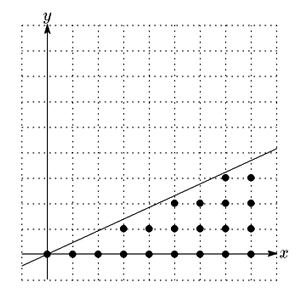
解答(1) $\displaystyle \lim_{n \to \infty}\dfrac{S_n}{n^2}=\dfrac{\sqrt{5}}{10}$を示せ.
(2) 以下の条件($\mathrm{H}$)を満たすような実数$C$は存在しないことを示せ.
($\mathrm{H}$) すべての自然数$n$について,$ \left|S_n- \dfrac{\sqrt{5}n^2}{10}\right|< C $ が成立する.