東北大AOII期 1番解答
(1)
関数 $ y=x^{\frac{1}{x}} $ を, $ x>e $ で考える.
\[
\log y=\dfrac{1}{x}\log x
\]
なので,両辺を $ x $ で微分する.
\[
\dfrac{y'}{y}=-\dfrac{1}{x^2}\log x+\dfrac{1}{x^2}=\dfrac{1}{x^2}\left(1-\log x \right)
\]
よって, $ x >e $ において $ \dfrac{y'}{y} $ は負. $ y >0 $ なので, $ y'< 0 $ である.
したがって,関数 $ y=x^{\frac{1}{x}} $ は $ x >e $ において単調減少である.
よって, $ a,b\geqq 3 >e $ のとき,
$ a< b $ と $ a^{\frac{1}{a}}>b^{\frac{1}{b}} $ は同値である.
(2) \[ a_n=\sqrt[n]{ \left\{1+\left(\dfrac{1}{n}\right)^2\right\} \left\{1+\left(\dfrac{2}{n}\right)^2\right\} \cdots \left\{1+\left(\dfrac{n}{n}\right)^2\right\}} \] であるから, \[ \log a_n=\dfrac{1}{n}\sum_{k=1}^n\log\left\{1+\left(\dfrac{k}{n}\right)^2 \right\} \] となる. よって \begin{eqnarray*} \lim_{n \to \infty}\log a_n&=&\int_0^1\log\left(1+x^2 \right)\,dx\\ &=&\left[x\log (1+x^2) \right]_0^1-\int_0^1x\cdot \dfrac{2x}{1+x^2}\,dx\\ &=&\log 2-2\int_0^1\left(1-\dfrac{1}{1+x^2} \right) \end{eqnarray*} 定積分 $ \displaystyle \int_0^1\dfrac{1}{1+x^2}\,dx $ において, $ x=\tan\theta $ と置換すると, $ \displaystyle \dfrac{1}{1+x^2}=\cos^2\theta $ で, $ \displaystyle \dfrac{dx}{d\theta}=\dfrac{1}{\cos^2\theta} $ なので, \[ \int_0^1\dfrac{1}{1+x^2}\,dx=\int_0^{\frac{\pi}{4}}1\,d\theta=\dfrac{\pi}{4} \] である.これより, \[ \lim_{n \to \infty}\log a_n=\log 2-2+\dfrac{\pi}{2} \] となる. 関数 $ \log x $ は連続なので, \[ \lim_{n \to \infty}a_n=e^{\log 2-2+\frac{\pi}{2}} =2e^{-2+\frac{\pi}{2}} \] である.
(3)
直線 $ y=(2t-2)x-t^2-1 $ の式を $ t $ で整理すると,
$ t^2-2xt+2x+y+1=0 $ となるので,
点 $ (x,\ y) $ が直線の通過する領域にあるための必要十分条件は,
\[
t^2-2xt+2x+y+1=0,\ \quad 0\leqq t \leqq 1
\]
となる $ t $ が存在することである.
$ f(t)=t^2-2xt+2x+y+1 $ とおくと,次のいずれかが成立することである.
\begin{eqnarray*}
① && f(0)\leqq 0,\ f(1)\geqq 0\\
② && f(0)\geqq 0,\ f(1)\leqq 0\\
③ && f(0)\geqq 0,\ f(1)\geqq 0,\ 0\leqq x \leqq 1,\ 判別式\ D\geqq 0
\end{eqnarray*}
$ f(0)=2x+y+1 $ , $ f(1)=y+2 $ , $ D/4=x^2-2x-y-1 $ なので,
\begin{eqnarray*}
① && 2x+y+1\leqq 0,\ y+2\geqq 0\\
② && 2x+y+1\geqq 0,\ y+2\leqq 0\\
③ && 2x+y+1\geqq 0,\ y+2\geqq 0,\ 0\leqq x \leqq 1,\ y\geqq x^2-2x-1
\end{eqnarray*}
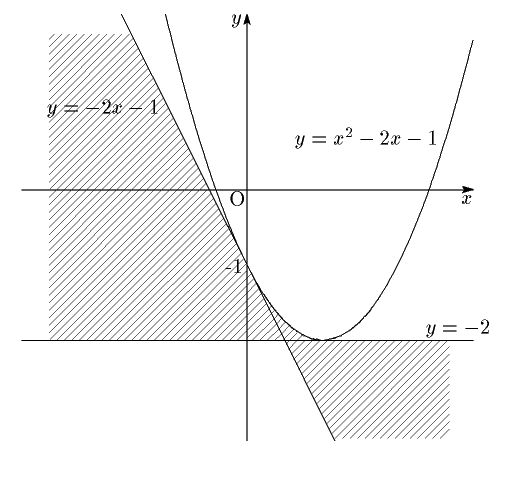
となる.これを図示する.