複素平面上に原点 ![]() と,2点
と,2点
![]() がある.
がある.
さらに
![]() の辺
の辺
![]() ,
, ![]() ,
, ![]() 上に点
上に点
![]() ,
,
![]() ,
,
![]() をとる.
をとる.
-
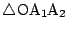 の面積は
の面積は
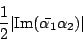
であることを示せ. - 線分
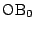 ,
,
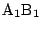 ,
,
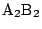 を
を
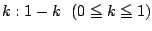 に内分する点を
に内分する点を 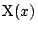 ,
, 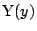 ,
, 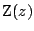 とし,
とし,
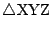 の面積を
の面積を 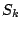 とする.
とする. 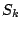 を
を 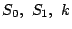 で表せ.
で表せ.
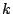 を0から1まで変化させるとき,途中で
を0から1まで変化させるとき,途中で 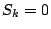 となることが起こるための条件を
となることが起こるための条件を 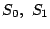 を用いて表せ.
を用いて表せ.
複素平面上に原点 ![]() と,2点
と,2点
![]() がある.
がある.
さらに
![]() の辺
の辺
![]() ,
, ![]() ,
, ![]() 上に点
上に点
![]() ,
,
![]() ,
,
![]() をとる.
をとる.