![]() は
は ![]() を満たす正の定数とする.
を満たす正の定数とする.
![]() 平面の二つの円
平面の二つの円
![]() がある.
がある.
![]() 上の一点
上の一点 ![]() から
から ![]() にひとつの接線をひき,その延長が再び
にひとつの接線をひき,その延長が再び ![]() と交わる
点を
と交わる
点を ![]() とする.
とする. ![]() から
から ![]() に
に ![]() とは異なる接線をひき,
その延長が再び
とは異なる接線をひき,
その延長が再び ![]() と交わる点を
と交わる点を ![]() とする.
とする. ![]() から
から ![]() に
に ![]() とは異なる接線をひき,その延長が再び
とは異なる接線をひき,その延長が再び ![]() と交わる点を
と交わる点を ![]() とする.
とする.
-
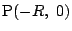 のとき,
のとき,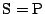 となった.
となった.
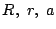 の間に成り立つ関係を求めよ.
の間に成り立つ関係を求めよ.
- 実数
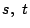 に対し
に対し
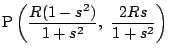 と
と
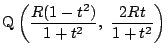 は
は
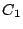 上の2点である.
直線
上の2点である.
直線 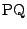 が円
が円 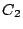 に接するための条件を
に接するための条件を 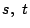 の多項式で表せ.
の多項式で表せ.
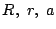 の間に(1)で求めた関係式が成り立つとき,任意の点
の間に(1)で求めた関係式が成り立つとき,任意の点 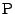 に対して
に対して
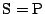 となることを示せ.
となることを示せ.