一般化された問題を解け.
原題(98年の京大)
袋に青色,赤色,白色の形の同じ玉がそれぞれ 3 個ずつ入っている.各色の 3 個の玉にはそれぞれ
1 , 2 , 3 の番号がついている.これらの 9 個の玉をよくかきまぜて袋から同時に 3 個の玉を取り出す.
取り出した 3 個のうちに同袋の中に青色,赤色,白色の形の同じ玉がそれぞれ3個ずつ入っている.
各色の3この玉には,それぞれ1,2,3の番号がついている.
これら9個の玉をよくかきまぜて復路から同時に3個の玉を取り出す.
取り出した3個のうちに同色のものが他になく,同番号のものも他にない玉の個数を得点とする.
たとえば,青1番,赤1番,白3番を取り出したときの得点は1で,
青2番,赤2番,赤3番を取り出したときの得点は0である.このとき以下の問いに答えよ.
- 得点が
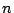 になるような取り出し方の数を
になるような取り出し方の数を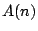 とするとき,
とするとき,
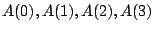 を求めよ.
を求めよ.
- 得点の期待値を求めよ.
一般化
袋に,![]() 種の色でぬられた同じ形の玉が
種の色でぬられた同じ形の玉が![]() 個ずつ
個ずつ![]() 個入っている.
各色の
個入っている.
各色の![]() 個の玉には 1 から
個の玉には 1 から![]() まで番号がついている.ここから同時に
まで番号がついている.ここから同時に![]() 個の玉を取り出す.
個の玉を取り出す.
![]() 個のうち同色のものが他になく,同番号のものも他にない玉の個数を得点とする.
個のうち同色のものが他になく,同番号のものも他にない玉の個数を得点とする.
得点が ![]() になるような取り出し方の総数を
になるような取り出し方の総数を ![]() とする.
とする.
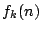 を求める一般的な方法を見いだし,
を求める一般的な方法を見いだし,
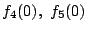 を求めよ.
を求めよ.
- 得点の期待値を
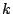 の式で表せ.
の式で表せ.
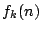 を
を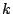 と
と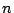 の式で表すことはできるか.
の式で表すことはできるか.