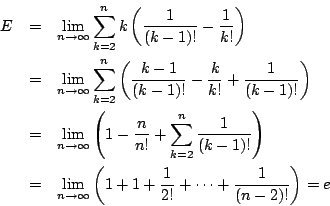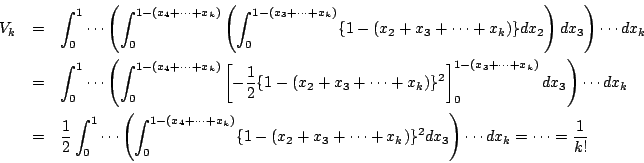上: 確率分野
前: その他確率の有名問題
解答 4.1
問題
4.1
 の関係式を作る.
の関係式を作る.
得点が となるためには,同色同番が他にないものが
となるためには,同色同番が他にないものが 個なので,まずこの
個なので,まずこの 個を決める.
そのために
個を決める.
そのために から一つとり,その色と番号が違う
から一つとり,その色と番号が違う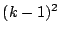 から一つとり,順次
から一つとり,順次 個目を
個目を
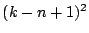 個から一つとる.このとり方の総数は,
個から一つとる.このとり方の総数は, 個の順序に関係ないから
個の順序に関係ないから
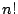 でわって,
でわって,
残る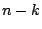 個は互いに同色同番があるような選び方だから,
個は互いに同色同番があるような選び方だから,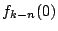 通り.よって,
通り.よって,
ただし,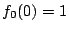 とする.
とする.
得点は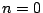 から
から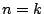 のいずれかであるから,これらにわたる和は,選び方の総数
のいずれかであるから,これらにわたる和は,選び方の総数
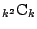 に一致する.
に一致する.
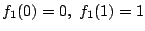 である.
である.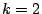 のとき,
のとき,
これから
以下順に,各 にたいし,
にたいし,
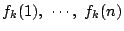 を求め,漸化式から
を求め,漸化式から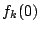 を求める.
それを用いて
を求める.
それを用いて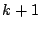 の列を求める.その結果は
の列を求める.その結果は
となる.
- (以下はKaney さんによる)
となる.ゆえに
従って求める期待値は
となる.
- (行列を使う Kaney さんの方法)
以下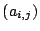 で
で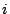 行
行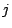 列成分が
列成分が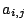 の行列を表す.
の行列を表す.
なので行列表示で
となる.さらに
であることがわかる.なぜなら
であるから
となるからである.
したがって
となる.
注
(3)は生成関数の方法でもできる.生成関数については『数学対話』「生成関数の方法(1)」を見てほしい.
生成関数方法は,数列を求めるのに大変強力な方法なのだ.
解答 4.2
問題
4.2
 回目に赤,他は青となる確率を
回目に赤,他は青となる確率を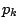 とおく.
とおく.
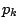 を求める.次式ででは
を求める.次式ででは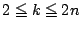 とする.
とする.
これらは互いに排反事象である.ゆえに求める確率は
- 赤から交互に発色する確率は
同様に青から交互に発色する確率も
 .
ゆえに
.
ゆえに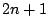 回発色するとき,2色が交互に発色する確率は
回発色するとき,2色が交互に発色する確率は
 回目の発色が赤である確率を
回目の発色が赤である確率を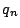 とする.このとき
とする.このとき
これから
ここで
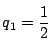 であるから,これを代入して整理する.
であるから,これを代入して整理する.



解答 4.4
問題
4.4
- 2回目以降は常に,1回勝ってこれから次の勝負をする者,
0回勝ってこれから次の勝負をする者,待っている者,がいる.
それぞれが優勝する確率を
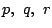 とする.すると次の連立方程式が成り立つ.
とする.すると次の連立方程式が成り立つ.
これを解いて
を得る.よって,それぞれが優勝する確率は次のようになる.
- 2回目以降,4人はつぎのいずれかの状態におかれる.
状態イ
2回勝ってこれから次の勝負をする者,0回勝ってこれから次の勝負をする者,
この勝負を待っている者1,この勝負を待っている者2.
状態ロ
1回勝ってこれから次の勝負をする者,0回勝ってこれから次の勝負をする者,
この勝負を待っている者1,この勝負を待っている者2.
状態イのそれぞれが優勝する確率を順に
状態ロのそれぞれが優勝する確率を順に
とする.すると次の連立方程式が得られる.
これを解く.
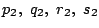 を消去して,
を消去して,
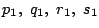 について解くと,
について解くと,
を得る.よって,それぞれが優勝する確率は次のようになる.
- 勝ち拔きの問題が一般的に解かれました.2002年9月14日付連絡ありました.
Web頁『数学初段』が閉鎖されたのでいただいたファイルで紹介します.
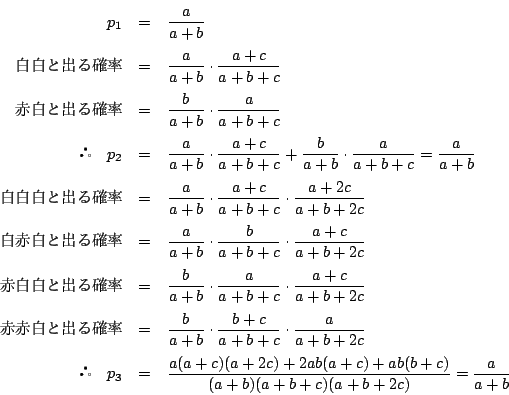
よって
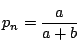 と推測される. これを数学的帰納法で証明する.
と推測される. これを数学的帰納法で証明する.
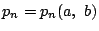 とおき,任意の
とおき,任意の 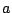 と
と 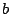 について
について
が成り立つことを

についての帰納法で示す.
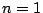 のとき.(1)より示されている.
のとき.(1)より示されている.
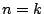 のとき成立するとする.
のとき成立するとする.
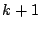 回目に白が出る場合を,1回目の色で分類する.
回目に白が出る場合を,1回目の色で分類する.
よって
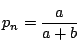 が成立する.
が成立する.
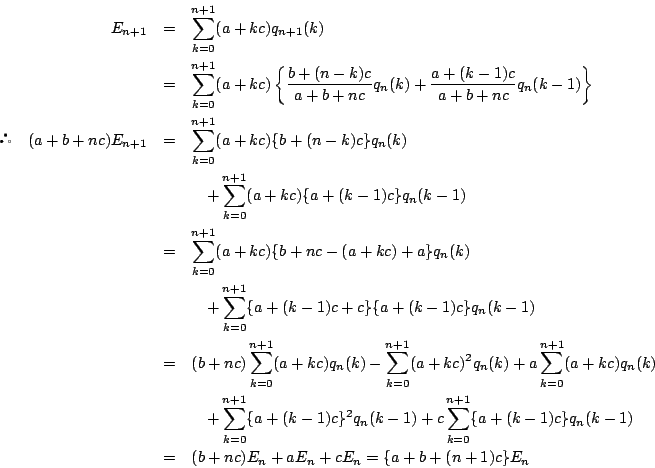
したがって
ここで
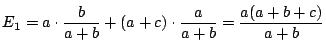 より
より

事象の総数は,
このうち白が 回,赤が
回,赤が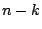 回出る出方は
回出る出方は
したがって確率は
解答 4.6
問題
4.6
- 線分の長さを1にして一般性を失わない.長さ
 と
と 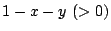 に切断したとする.こうして得られた3本の線分が三角形を作る条件は
に切断したとする.こうして得られた3本の線分が三角形を作る条件は
 である.
である.
従って求める確率は
領域
の面積に対する,領域
の面積の比である.(図1)
従って求める確率は
- 3本の線分の長さを1にしてよい.取り出された各線分の長さを
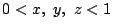 とする.こうして得られた3本の新たな線分が三角形を作る条件は
とする.こうして得られた3本の新たな線分が三角形を作る条件は
 従って求める確率は
立方体
従って求める確率は
立方体
の体積に対する,立体
の体積の比である.
 の体積を求める.
の体積を求める.  での切断面は図2のようになりその面積は
での切断面は図2のようになりその面積は
よって 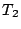 の体積は
の体積は
従って求める確率は
- (1)のもとで得られた3本の線分が鋭角三角形を作る条件は
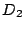 の条件に加えて
の条件に加えて
 である.その領域を
である.その領域を 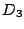 とする.この条件は
とする.この条件は
と書き表される.
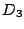 の面積(境界を含む)は,
の面積(境界を含む)は, 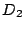 の面積から,図3の領域(イ)一つ,と領域(ロ)を二つ分を減じたものである.
の面積から,図3の領域(イ)一つ,と領域(ロ)を二つ分を減じたものである.
(イ)の面積は
となりこれは(ロ)の面積に等しい.この値を求める.
ゆえに 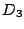 の面積は
の面積は
従って3本の線分が鋭角三角形を作る確率は
- (2)のもとで得られた3本の線分が鋭角三角形を作る条件は
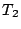 の条件に加えて
の条件に加えて
 である.この立体を
である.この立体を 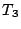 とする.
とする.
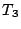 の体積(境界を含む)をもとめる.
の体積(境界を含む)をもとめる. 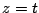 での切断面において,
での切断面において, 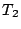 の切断面から,
図4の領域(ハ)一つ,と領域(ニ)を二つ分を減じたものである.
の切断面から,
図4の領域(ハ)一つ,と領域(ニ)を二つ分を減じたものである.
(ハ)の面積は
したがって 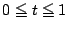 を動かすときその体積は
を動かすときその体積は
(ニ)のの部分から定まる体積は条件の対称性から(ハ)の部分から定まる体積に等しい.
ゆえに 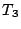 の面積は
の面積は 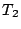 の体積が
の体積が 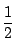 であったので,
であったので,
従って3本の線分が鋭角三角形を作る確率は
解答 4.7
問題
4.7
 長さが
長さが 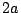 の針の中点が一つの直線から
の針の中点が一つの直線から 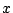 の距離のところに落ちるとする.
針と,直線と直交する方向のなす角を
の距離のところに落ちるとする.
針と,直線と直交する方向のなす角を 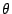 とする.対称性を考慮し
とする.対称性を考慮し
としてよい.
このときこのとき針がこの直線と交わるのは
のときである.
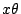
平面の領域
のなかで
領域
の占める面積は
ゆえに求める確率は 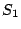 の面積が
の面積が
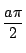 であるから
であるから
【問題甲】
解法1
余事象で考える. $ 1 $ から $ n $ までの番号のついたカード $ n $ 枚を勝手に並べるとき,
各 $ k\ (1\leqq k \leqq n) $ について $ k $ 番目に番号 $ k $ のカードがないような並べ方の総数を $ C(n) $ とおく.
$ n $ 枚のカードの順列を1番目と $ n $ 番めのカードで場合に分ける.
(i) $ n $ 番目のカードは1から $ n-1 $ のいずれかである.この場合分けが $ n-1 $ 通り.
(ii) 1番目のカードに $ n $ がこない場合.この場合,この $ n $ を1と読み替えると
1から $ n-1 $ のカードがそれぞれ番号と同じ位置にこない並べ方だけある. $ C(n-1) $ 通り.
(iii) 1番目のカードが $ n $ の場合.この場合,2から $ n-1 $ が2番から $ n-1 $ 番にこない
並べ方である.この場合,カードの数と位置の番号からそれぞれ1減じれば,
1から $ n-2 $ が1番から $ n-2 $ 番にこない並べ方と同じである.ゆえに $ C(n-2) $ 通り.
\[
∴ C(n)=(n-1)\{C(n-1)+C(n-2)\}
\]
各 $ k \ (1\leqq k \leqq n) $ について $ k $ 番目に番号 $ k $ のカードがない事象の確率を $ p_n $ とおく. $ n $ 枚の並べ方は $ n! $ 通りある.したがって
\begin{eqnarray*}
p_n&=&\dfrac{C(n)}{n!}=\dfrac{(n-1)\{C(n-1)+C(n-2)\}}{n!}\\
&=&\dfrac{n-1}{n}p_{n-1}+\dfrac{1}{n}p_{n-2}
\end{eqnarray*}
である.これから,
\[
p_{n+2}-p_{n+1}=\dfrac{1}{n+2}\left(p_n-p_{n+1} \right)
=-\dfrac{1}{n+2}\left(p_{n+1}-p_n \right)
\]
つまり,
\[
p_{n+1}-p_n=
\dfrac{(-1)^{n-1}\cdot2}{(n+1)!}(p_2-p_1)
=\dfrac{(-1)^{n-1}\cdot2}{(n+1)!}\cdot\dfrac{1}{2}
=\dfrac{(-1)^{n-1}}{(n+1)!}
\]
となる.よって,
\[
p_n=\dfrac{1}{2!}-\dfrac{1}{3!}+\dfrac{1}{4!}-\cdots+\dfrac{(-1)^n}{n!}
\]
となる.したがって,求める確率は
\[
1-p_n=1-\dfrac{1}{2!}+\dfrac{1}{3!}-\dfrac{1}{4!}+\cdots+\dfrac{(-1)^{n-1}}{n!}
\]
である.
また,次式も成立する.
\[
\lim_{n \to \infty}p_n=\dfrac{1}{e}
\]
解法2
事象の総数は $ n! $ である.
少なくとも一枚 $ k $ 番目に番号 $ k $ のカードのある並べ方の総数を $ f(n) $ とおく.
どの番号に同じカードが来るかを決め,他は任意に並べると,その並べ方は,
\[
{}_n \mathrm{C}_1(n-1)!
\]
ある.ここには,2ヵ所に同じカードがある場合が,2重に数えられている.そこで,
\[
{}_n \mathrm{C}_1(n-1)!-{}_n \mathrm{C}_2(n-2)!
\]
とすると,3ヵ所に同じカードがある場合が,
\[
{}_3 \mathrm{C}_1-{}_3 \mathrm{C}_2=0
\]
となり,数えられていない.
そこで,
\[
{}_n \mathrm{C}_1(n-1)!-{}_n \mathrm{C}_2(n-2)!+{}_n \mathrm{C}_3(n-3)!
\]
とすると,3ヵ所に同じカードがある場合までは正しく数えられている.
以下,
\[
0=(1-1)^k=1+\sum_{j=1}^{k-1}{}_k \mathrm{C}j(-1)^j+(-1)^k
\]
より,
\[
\sum_{j=1}^{k-1}{}_k \mathrm{C}_j(-1)^{j-1}=1+(-1)^k
\]
であるから,
\begin{eqnarray*}
f(n)&=&\sum_{k=1}^n(-1)^{k-1}{}_n \mathrm{C}_k(n-k)!\\
&=&n\cdot(n-1)!-\dfrac{n(n-1)}{2}\cdot(n-2)!+\cdots\\
&& +(-1)^{k-1}\dfrac{n!}{k!(n-k)!}\cdot(n-k)!+\cdots+(-1)^{n-1}\\
&=&n!-\dfrac{n!}{2!}+\cdots+(-1)^{k-1}\dfrac{n!}{k!}+\cdots+(-1)^{n-1}\dfrac{n!}{n!}\\
\end{eqnarray*}
よって,
\begin{eqnarray*}
1-p_n&=&\dfrac{f(n)}{n!}\\
&=&1-\dfrac{1}{2!}+\dfrac{1}{3!}-\dfrac{1}{4!}+\cdots+\dfrac{(-1)^{n-1}}{n!}
\end{eqnarray*}
を得る.
【問題乙】
$ C(n) $ について.
$ 1 $ から $ n $ までの番号のついた赤球と白球,あわせて $ 2n $ 個を,円周上に無作為に並べるとき,
赤球と白球が隣りあうことはなく,
かつ同じ番号の赤球と白球が隣りあうことがないような並べ方の総数が $ C(n) $ である.
$ C(1)=0 $ , $ C(2)=0 $ である.
$ n=3 $ のときは,赤球3個を並べれば白球3個のおき方は1通り.よって, $ C(3)=2 $ .
$ n\geqq 4 $ とする.
赤1に隣りあう白球の番号を $ k $ とする. $ k $ の選び方は $ n-1 $ 通りである.
(1) 赤球 $ k $ と白球1が隣りあう場合.これらを除いた赤球,白球それぞれ $ n-2 $ 個の並べ方が $ C(n-2) $ 通り.
その $ 2n-4 $ 個の玉の間のどこに赤1白 $ k $ と赤 $ k $ 白1をおくかが $ {}_{2n-4} \mathrm{C}_2 $ 通り.よってこの場合は
\[
(n-1)C(n-2)(n-2)(2n-5)\ (通り)
\]
(2) 赤球 $ k $ と白球1が隣りあわない場合.
赤1白球 $ k $ を除く $ 2n-2 $ 個で,同じ番号は隣りあわず赤球 $ k $ と白球1も隣りあわない並べ方は $ C(n-1) $ 通り.
ここに赤1白 $ k $ を入れるが,赤 $ k $ ,白1の横にもおけないので, $ 2n-2-4 $ 通り.よってこの場合は
\[
(n-1)C(n-1)(2n-6)\ (通り)
\]
\[
∴ C(n)=(n-1)(n-2)(2n-5)C(n-2)+(n-1)(2n-6)C(n-1)
\]
$ f(n) $ について.
少なくとも $ k $ 組,同じ番号の赤球と白球が隣りあう場合の数を求める.
$ k $ 組みの決め方が $ {}_n \mathrm{C}_k $ 通り.それらを除く $ 2(n-k) $ を並べるのは,
$ (n-k-1)!(n-k)! $ 通り.
そこに $ k $ 個の赤球をおく.赤球をおけば白玉のおき方は1通り.
それは
\[
(2n-2k)(2n-2k+1)\cdots(2n-k-1)
\]
の $ k $ 個の積である.よって,
\begin{eqnarray*}
&&{}_n \mathrm{C}_k\cdot (n-k-1)!(n-k)!\cdot(2n-2k)(2n-2k+1)\cdots(2n-k-1)\\
&=&\dfrac{n!}{k!}2(n-k)!(2n-2k+1)\cdots(2n-k-1)
\end{eqnarray*}
ある.
問題甲の解法2と同様に
\[
f(n)=\sum_{k=1}^n(-1)^{k-1}\dfrac{n!}{k!}2(n-k)!(2n-2k+1)\cdots(2n-k-1)
\]
となる.
例
\begin{eqnarray*}
C(4)&=&(4-1)(4-2)(8-5)C(2)+(4-1)(8-6)C(3)=12\\
f(4)&=&24\cdot2\cdot6-12\cdot2\cdot2\cdot5+4\cdot2\cdot3\cdot4-2\cdot2\cdot3=132\\
3!4!&=&C(4)+f(4)\\
C(5)&=&(5-1)(5-2)(10-5)C(3)+(5-1)(10-6)C(4)=312\\
f(5)&=&120\cdot2\cdot24-60\cdot2\cdot6\cdot7+20\cdot2\cdot2\cdot5\cdot6\\
&&\quad \quad -
5\cdot2\cdot3\cdot4\cdot5+2\cdot2\cdot3\cdot4=2568\\
4!5!&=&C(5)+f(5)
\end{eqnarray*}
【問題丙】
ここで用いた方法は,少し異なる設定でも用いられる.
各々の客車に少なくとも1人は乗るような乗り方は何通りあるかを次のように,2通りの方法で考える.
1) 明らかに, $ n< m $ なら0通り, $ n=m $ なら各客車に1人ずつ乗るので, $ m! $ 通りである.
2) すべての乗り方は,それぞれの乗客が $ m $ 通り選べるので, $ m^n $ 通りある.
ここから,乗らない客車がある場合の総数を引く.
乗らない客車が1輌の場合. $ {}_m \mathrm{C}_1(m-1)^n $ 通り.
この中では,乗らない客車が2輌の場合が2重に数えられている.
よって,乗らない客車が1輌か2輌の場合は
\[
{}_m \mathrm{C}_1(m-1)^n-{}_m \mathrm{C}_2(m-2)^n
\]
通りある.
この中では乗らない客車が3輌の場合が $ 3-3=0 $ になっている.
よって,乗らない客車が1〜3輌の場合は
\[
{}_m \mathrm{C}_1(m-1)^n-{}_m \mathrm{C}_2(m-2)^n+{}_m \mathrm{C}_3(m-3)^n
\]
通りとなる.以下,
\[
0=(1-1)^k=1+\sum_{j=1}^{k-1}{}_k \mathrm{C}j(-1)^j+(-1)^k
\]
より,
\[
\sum_{j=1}^{k-1}{}_k \mathrm{C}_j(-1)^{j-1}=1+(-1)^k
\]
となるので,これをもとに,同様に数える.
乗らない客車が $ k-1 $ までの和の中で $ 1+(-1)^k $ 回数えられているので,
$ k $ 回目に $ {}_m \mathrm{C}_k(-1)^{k-1}(m-k)^n $ を加える.
この結果,乗らない客車がある場合の総数は
\[
\sum_{k=1}^{m-1}{}_m \mathrm{C}_k(-1)^{k-1}(m-k)^n
\]
となる.したがって,
\begin{eqnarray*}
a_m(n)&=&m^n-\sum_{k=1}^{m-1}{}_m \mathrm{C}_k(-1)^{k-1}(m-k)^n
=m^n+\sum_{k=1}^{m-1}{}_m \mathrm{C}_k(-1)^k(m-k)^n\\
&=&\sum_{k=0}^{m-1}{}_m \mathrm{C}_k(-1)^k(m-k)^n
=\sum_{k=0}^{m-1}{}_m \mathrm{C}_{m-k}(-1)^k(m-k)^n\\
&=&\sum_{k=1}^{m}{}_m \mathrm{C}_k(-1)^{m-k}k^n\ (順を逆にした)\\
&=&(-1)^m\sum_{k=1}^{m}{}_m \mathrm{C}_k(-1)^kk^n\\
&=&\sum_{k=1}^{m}{}_m \mathrm{C}_k(-1)^{m-k}k^n
\end{eqnarray*}
となる.
これからまた,等式
\[
\sum_{k=1}^m{}_m\mathrm{C}_k (-1)^{m-k}k^n
=
\left\{
\begin{array}{ll}
0&(n< m)\\
m!&(n=m)
\end{array}
\right.
\]
も成りたつ.
方法2
すべての乗り方は, $ m^n $ 通りある.これを,何台の客車に乗るかで分けることにより,
\[
m^n=\sum_{k=1}^{m}{}_m \mathrm{C}_ka_k(n)
\]
である.東工大2004年後期の解答にあるように,
0以上の整数で定義された2つの数列 $\{a_n \},\ \{b_n\} $ の間の関係式,
\[
b_m=\sum_{k=0}^m{}_n\mathrm{C}_ka_k
\]
\[
a_m=\sum_{k=0}^m(-1)^{m-k}{}_m\mathrm{C}_kb_k
\]
は同値である.これを $ b_m=m^n $ , $ a_m=a_m(n) $ で用いることにより,
\[
a_m(n)=\sum_{k=0}^m(-1)^{m-k}{}_m\mathrm{C}_kk^n
\]
がなり立つ.
方法3
特定の乗客Aについて,次の2つの場合を考える.
Aがある客車に1人で乗るとき.
その客車の選び方が $ m $ 通り.それを除く $ m-1 $ 台の客車にAを除く $ n-1 $ 人が乗るので,
$ ma_{m-1}(n-1) $ 通り.
Aが他の誰かと乗る場合.
まずA以外の $ n-1 $ 人を $ m $ 台に乗せる.そして何れかにAも乗る.
その場合の数は $ ma_{m}(n-1) $ 通り.
よって,
\[
a_m(n)=m\left\{a_{m-1}(n-1)+a_m(n-1) \right\}
\]
がなり立つ.これをもとに
\[
a_m(n)
=(-1)^m\sum_{k=1}^{m}{}_m \mathrm{C}_k(-1)^kk^n
=\sum_{k=1}^{m}{}_m \mathrm{C}_k(-1)^{m-k}k^n
\]
が,すべての0以上の整数 $ m $ に対し成立することを,
$ n $ についての数学的帰納法で示す.
定義から $ a_1(n)=1 $ , $ m\ge 2 $ のとき, $ a_m(1)=0 $ である.
$ m=n=1 $ のとき,
\[
\sum_{k=1}^{m}{}_m \mathrm{C}_k(-1)^{m-k}k^n
=1
\]
である.
一方, $ m\ge 2 $ のとき,二項定理
\[
(1-x)^m=\sum_{k=0}^{m}{}_m \mathrm{C}_k(-x)^k
\]
の両辺を $ x $ で微分すると,
\[
-(1-x)^{m-1}=\sum_{k=1}^{m}{}_m \mathrm{C}_k(-1)^k\cdot kx^{k-1}
\]
となる.ここで $ x=1 $ を代入することにより,
\[
0=\sum_{k=1}^{m}{}_m \mathrm{C}_k(-1)^k k
\]
これより,
\[
a_m(1)=\sum_{k=1}^{m}{}_m \mathrm{C}_k(-1)^{m-k}k^1=0
\]
となり, $ n=1 $ のとき成立する.
$ n-1 $ までは成立するとする.
\begin{eqnarray*}
a_m(n)&=&m\left\{a_{m-1}(n-1)+a_m(n-1) \right\}\\
&=&m\left\{\sum_{k=1}^{m-1}{}_{m-1} \mathrm{C}_k(-1)^{m-1-k}k^{n-1}
+\sum_{k=1}^{m}{}_m \mathrm{C}_k(-1)^{m-k}k^{n-1} \right\}\\
&=&m\sum_{k=1}^{m-1}(-1)^{m-1-k}k^{n-1}\left({}_{m-1} \mathrm{C}_k-{}_m \mathrm{C}_k \right)
+k^{n-1}
\end{eqnarray*}
ここで,
\[
{}_{m-1} \mathrm{C}_{k-1}+{}_{m-1} \mathrm{C}_k={}_m \mathrm{C}_k
\]
なので.
\begin{eqnarray*}
a_m(n)&=&m\sum_{k=1}^{m-1}(-1)^{m-k}k^{n-1}{}_{m-1} \mathrm{C}_{k-1}+k^{n-1}\\
&=&m\sum_{k=1}^{m}(-1)^{m-k}k^{n-1}{}_{m-1} \mathrm{C}_{k-1}
\end{eqnarray*}
さらに,
\[
m{}_{m-1} \mathrm{C}_{k-1}=k{}_m \mathrm{C}_k
\]
なので,
\begin{eqnarray*}
a_m(n)&=&\sum_{k=1}^{m}(-1)^{m-k}k^n{}_m\mathrm{C}_k
\end{eqnarray*}
となり, $ n $ でも成立することが示された.
よってすべての自然数 $ n $ に対して成立する.
2004年東工大後期,
2007年名古屋市大,
2014年大阪医大を参照のこと.
解答 4.9
問題4.9
【問題甲】
 回の試行で記録された数字の合計が
回の試行で記録された数字の合計が より大きい事象は,
数字の合計が
より大きい事象は,
数字の合計が 以下である事象の余事象である.
以下である事象の余事象である.
 回の試行で,数の選び方の総数は
回の試行で,数の選び方の総数は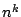 通りあり,いずれもが同様に確からしい.
通りあり,いずれもが同様に確からしい.
 回の試行で記録された数字の合計が
回の試行で記録された数字の合計が 以下である事象の総数を求める.
以下である事象の総数を求める.
不等式
をみたす正整数の組
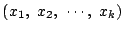 に対して
に対して
とおく.
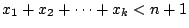 より
より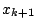 も正整数で
も正整数で
をみたす.
逆に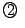 をみたす
正整数の組
をみたす
正整数の組
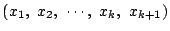 に対して
正整数の組
に対して
正整数の組
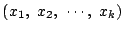 は
は をみたす.
をみたす.
ゆえに をみたす正整数解
をみたす正整数解
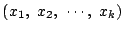 の個数と,
の個数と,
 をみたす正整数解
をみたす正整数解
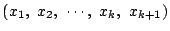 の個数は等しい.
の個数は等しい.
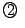 の解は,
の解は,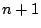 個の○を並べて,
個の○を並べて,
○と○の カ所の間
カ所の間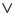 のうち
のうち カ所を選び,
カ所を選び,
 個の仕切りで区切って,
個の仕切りで区切って,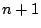 個の○を
個の○を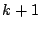 個の群に分ける分け方である.
その総数は
個の群に分ける分け方である.
その総数は
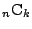 通りある.
通りある.
したがって 回の試行で記録された数字の合計が
回の試行で記録された数字の合計が 以下である確率は
以下である確率は
である.
ゆえに 回の試行で記録された数字の合計が
回の試行で記録された数字の合計が より大きい確率
より大きい確率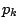 は,
は,
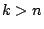 のとき
のとき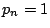 であるが,
であるが,
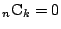 なので
なので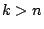 でも成立する.
また
でも成立する.
また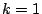 のとき和が
のとき和が より大きくなることはないが
より大きくなることはないが
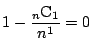 なので
なので
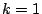 でも成立する.
でも成立する.
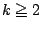 のとき,
のとき, 回の試行で記録された数字の合計がはじめて
回の試行で記録された数字の合計がはじめて
 より大きくなる事象は,
より大きくなる事象は, 回の試行で記録された数字の合計が
回の試行で記録された数字の合計が より大きい事象から
より大きい事象から
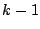 回の試行で記録された数字の合計が
回の試行で記録された数字の合計が より大きい事象を除いたものである.
ゆえにその確率
より大きい事象を除いたものである.
ゆえにその確率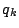 は
は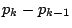 に等しい.
に等しい.
この式は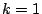 のとき0になるので,
のとき0になるので,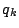 を表す等式は
を表す等式は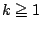 で成立する.
で成立する.
-
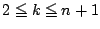 のとき
のとき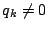 であるので期待値は次のようになる.
であるので期待値は次のようになる.
ここで
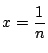 とおくと,
とおくと,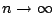 のとき
のとき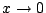 で
で
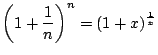 である.自然対数の底
である.自然対数の底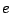 は
は
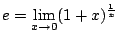 で定義される.
で定義される.
□
【問題乙】
注意
問題乙は問題甲を連続的な場合にしたものである.
この期待値も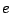 であることは次のような推論で予想がつく.
であることは次のような推論で予想がつく.
である.だから区間
から選ぶ数を,分母が
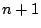
にとれる有理数にかぎると,そのような有理数の和が1より大きくなる回数の期待値が【問題甲】の
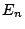
であることがわかる.
どのような実数も分母の大きい有理数をとれば任意の精度で近似できるので,
選ぶ数を実数にしたときの期待値は
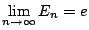 である.
である.
これを連続な確率の考えで解くと次のようになる.
解答
 回の試行で記録された数字の合計が1より大きい事象は,
数字の合計が1以下である事象の余事象である.
回の試行で記録された数字の合計が1より大きい事象は,
数字の合計が1以下である事象の余事象である.
 回目の試行で記録された数字を
回目の試行で記録された数字を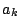 とする.
とする.
 回の試行で記録された数字の合計が1以下である事象の確率を求める.
回の試行で記録された数字の合計が1以下である事象の確率を求める.
 回の試行で記録された数字を
回の試行で記録された数字を
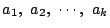 とする.
これは
とする.
これは 次元空間の点
次元空間の点
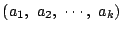 と見なせる.
すべての試行の結果は
と見なせる.
すべての試行の結果は
で表される

次元空間の領域
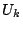
の各点に対応し,どの点の表す事象も同様に確からしい.
ただし
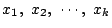
は

次元空間の座標系である.
和が1以下である事象に対応する領域は
である.この領域を
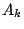
とする.
 回の試行で記録された数字の合計が1以下である事象の確率はこれら二つの領域の体積比である.
領域
回の試行で記録された数字の合計が1以下である事象の確率はこれら二つの領域の体積比である.
領域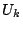 の体積は
の体積は
次に
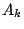
の体積を
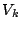
とおく.
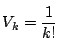
であることを示す.
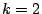
のとき.
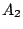
を
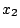
を固定してここで切ると切り口は
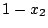
の線分である.
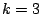
のとき.
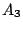
を
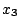
で切ると
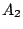
と相似で相似比が
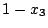
.面積比を考え
断面は面積
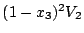
.
同様に
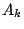
を
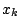
で切ると
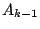
と相似で相似比が
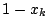
.体積比を考え
断面は体積
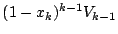
.
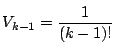
とすると
数学的帰納法によって
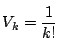
.
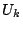 の体積が1なので,
の体積が1なので,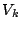 の値が
の値が 回の試行で和が1以下となる確率である.
回の試行で和が1以下となる確率である.
 回の試行で和が1より大きくなる確率を
回の試行で和が1より大きくなる確率を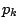 とすると
とすると
問題甲と同様に考え
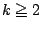
のとき

回の試行ではじめて和が1より大きくなる確率
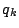
は
である.
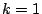
では1より大きくなることはありえない.
したがって,その期待値
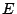
は
注意
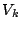 は次のように直接計算してもよい.
は次のように直接計算してもよい.



上: 確率分野
前: その他確率の有名問題
Aozora Gakuen
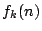 の関係式を作る.
の関係式を作る.
 となるためには,同色同番が他にないものが
となるためには,同色同番が他にないものが 個なので,まずこの
個なので,まずこの 個を決める.
そのために
個を決める.
そのために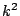 から一つとり,その色と番号が違う
から一つとり,その色と番号が違う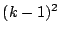 から一つとり,順次
から一つとり,順次 個目を
個目を
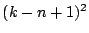 個から一つとる.このとり方の総数は,
個から一つとる.このとり方の総数は, 個の順序に関係ないから
個の順序に関係ないから
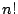 でわって,
でわって,
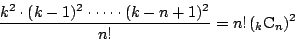
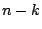 個は互いに同色同番があるような選び方だから,
個は互いに同色同番があるような選び方だから,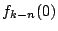 通り.よって,
通り.よって,
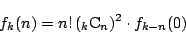
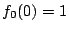 とする.
とする.
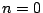 から
から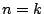 のいずれかであるから,これらにわたる和は,選び方の総数
のいずれかであるから,これらにわたる和は,選び方の総数
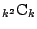 に一致する.
に一致する.
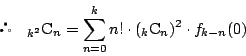
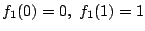 である.
である.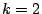 のとき,
のとき,
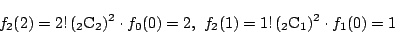
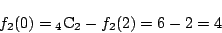
 にたいし,
にたいし,
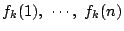 を求め,漸化式から
を求め,漸化式から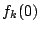 を求める.
それを用いて
を求める.
それを用いて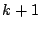 の列を求める.その結果は
の列を求める.その結果は

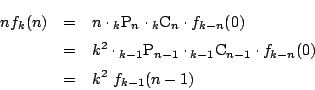
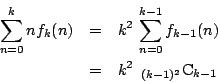
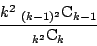
 で
で 行
行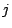 列成分が
列成分が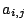 の行列を表す.
の行列を表す.
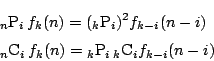
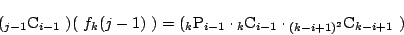
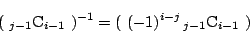
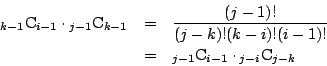
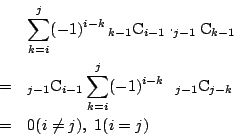
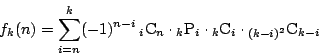
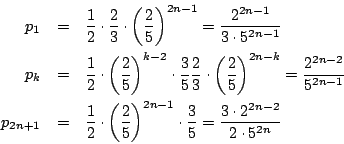
 .
ゆえに
.
ゆえに であるから,これを代入して整理する.
であるから,これを代入して整理する.



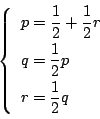
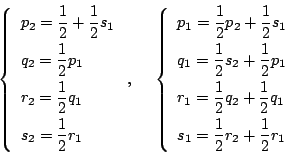
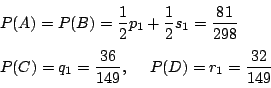
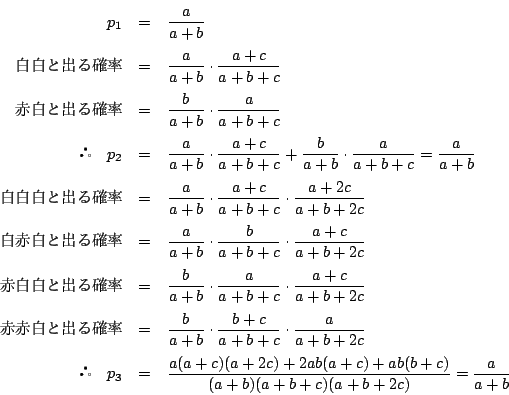
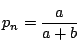 と推測される. これを数学的帰納法で証明する.
と推測される. これを数学的帰納法で証明する.
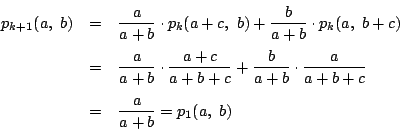
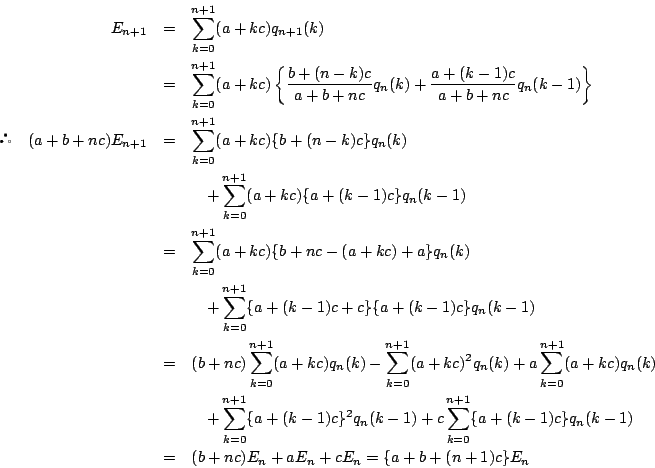
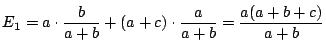 より
より

 である.
である.
 従って求める確率は
立方体
従って求める確率は
立方体
 である.その領域を
である.その領域を ![\begin{displaymath}
\int_0^{ \frac{1}{2}}\left(\dfrac{1}{2}+x- \dfrac{1}{2-2x}\r...
...1-x) \right]_0^{ \frac{1}{2}}
=\dfrac{3}{8}-\dfrac{1}{2}\log 2
\end{displaymath}](images/img878.gif)
 である.この立体を
である.この立体を  長さが
長さが 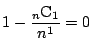 なので
なので
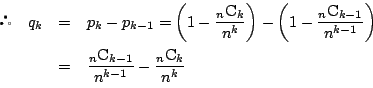
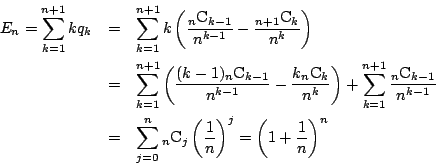
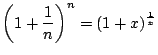 である.自然対数の底
である.自然対数の底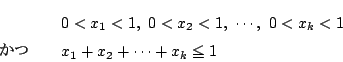
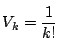 であることを示す.
であることを示す.
![\begin{displaymath}
V_2=\int_0^1(1-x_2)\,dx_2=\left[-\dfrac{(1-x_2)^2}{2} \right]_0^1=\dfrac{1}{2}
\end{displaymath}](images/img950.gif)
![\begin{displaymath}
V_3=\int_0^1(1-x_3)^2V_2\,dx_3=\left[-\dfrac{(1-x_3)^3}{3}V_2 \right]_0^1=\dfrac{1}{3!}
\end{displaymath}](images/img956.gif)
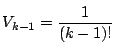 とすると
とすると
![\begin{displaymath}
V_k=\int_0^1(1-x_k)^{k-1}V_{k-1}\,dx_k=\left[-\dfrac{(1-x_k)^k}{k}V_{k-1} \right]_0^1
=\dfrac{1}{k}V_{k-1}=\dfrac{1}{k!}
\end{displaymath}](images/img962.gif)