![]() を実数係数の
を実数係数の ![]() 次の整式とする.
任意の整数
次の整式とする.
任意の整数 ![]() に対して
に対して![]() が整数値をとるための条件に関して次の問に答えよ.
が整数値をとるための条件に関して次の問に答えよ.
- 『任意の整数
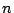 に対して,
に対して,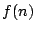 が整数となるための必要十分条件は
が整数となるための必要十分条件は
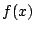 の
の 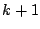 個の連続する整数
個の連続する整数
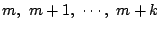 に対する値
に対する値
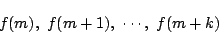
がすべて整数値である』ことを示そう.
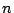 次の整式
次の整式 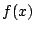 に対して
に対して
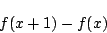
は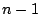 次以下であることを示せ.
次以下であることを示せ.
- 冒頭の命題を数学的帰納法で示せ.
- 0以上の整数
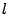 に対し
に対し
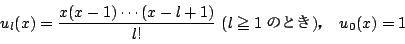
とおく.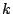 次多項式
次多項式 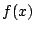 は実数
は実数
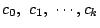 を用いて次のように表されることを示せ.
を用いて次のように表されることを示せ.
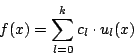
- 任意の整数
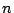 に対して
に対して 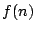 が整数となるための必要十分条件は,
が整数となるための必要十分条件は,
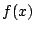 を上のように表したとき,
を上のように表したとき,
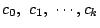 がすべて整数となることであることを示せ.
がすべて整数となることであることを示せ.