

 次: 二次曲面
上: 射影変換と複比
前: 射影空間での複比
次: 二次曲面
上: 射影変換と複比
前: 射影空間での複比
 命題 70
命題 70
完全四角形
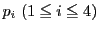
の対辺
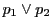
と
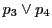
の交点を
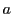
,
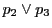
と
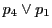
の交点を
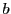
とし,
直線
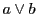
と対角線
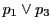
の交点を
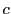
,
直線
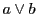
と対角線
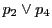
の交点を
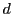
とする.
4点
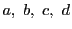
は
調和点列をなす.
■
証明
この関係は
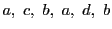 が四角性六点であることを意味し,
直線体
が四角性六点であることを意味し,
直線体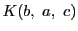 の点における和の定義21から
の点における和の定義21から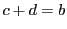 を意味する.
同型
を意味する.
同型
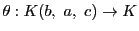 で
で
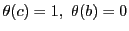 なので,
なので,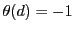 .つまり
.つまり
![$[a,\ b;\ c,\ d]=-1$](images/img1919.gif) である.
□
である.
□
証明
よって
![$[p_1,\ p_3;\ e,\ c]=-1$](images/img1925.gif) .
また
.
また
□
この系は,完全四角形のとり方を変えることで命題70の読み直しでも示される.
古典的な射影幾何で論証の主要な方法の一つが「対合」であった.
定義 27
射影直線
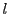
の恒等写像ではない射影変換

で,
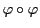
が恒等写像となるものを
対合という.
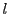 上の点
上の点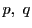 に対し,対合
に対し,対合 で
で
となるものが存在するとき,2点
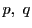
は
対合をなすという.
■
対合は行列でどのような形になるものなのか.
直線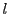 上に同次座標
上に同次座標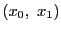 を設定する.
を設定する.
 を対合とする.可換体であるから,
を対合とする.可換体であるから, は
線型写像
は
線型写像
で表されるとしてよい.ただしこの行列は,
0行列でない二次行列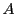 の集合を,
同値関係
の集合を,
同値関係
による商集合の同値類の代表である.
このとき,
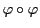 対応する行列の類は
対応する行列の類は
よってこの変換が恒等変換と同一の類に属する条件は
である.これから
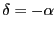 となる.
つまり対合である条件は,それを表す行列の類が
となる.
つまり対合である条件は,それを表す行列の類が
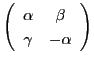 という形をしていて,
その行列式について
という形をしていて,
その行列式について
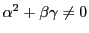 であることである.
であることである.
以下断らなくても直線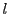 上の射影変換で考えるものとし,
さらに同次座標が設定されているものとする.
上の射影変換で考えるものとし,
さらに同次座標が設定されているものとする.
命題 71
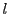
上の2点
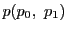
と
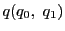
が
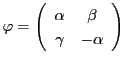
で対合をなすことは,関係式
が成り立つことと同値である.
■
証明
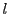 上の2点
上の2点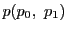 と
と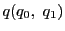 が
が
 で対合をなすことをいいかえると,
点
で対合をなすことをいいかえると,
点
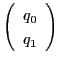 と
と
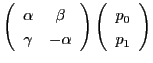 が同一の点となることである.よって
が同一の点となることである.よって
が条件である.これから命題の等式が成り立つ.
逆に命題の等式が成り立てば
2点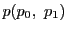 と
と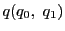 が
が
 で対合をなすことは,逆にたどることでわかる.
□
で対合をなすことは,逆にたどることでわかる.
□
命題 72
直線
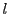
の射影変換

で
となる点
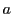
が存在すれば,

は対合である.
つまり任意の点
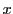
について
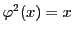
が成り立つ.
■
証明1
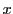 に対して
に対して
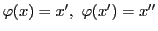 とおく.
また
とおく.
また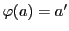 とする.このとき
とする.このとき
命題64より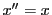 である.
□
である.
□
証明2
 に対応する行列を
に対応する行列を
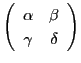 とおく.
点
とおく.
点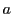 の非同次座標も
の非同次座標も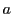 で表す.
条件から
で表す.
条件から
第2式から
第1式から
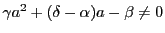 なので,
なので,
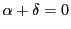 .つまり
.つまり は対合である.
□
は対合である.
□
系 72.1
異なる点の3組の点対
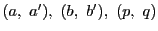
が対合をなす,
つまり
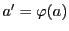
,
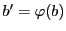
,
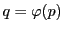
となる対合

が存在する条件は
となることである.
■
証明
命題72の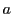 として,
として, をとれば
をとれば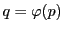 ,
,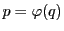 より
より は対合である.
□
は対合である.
□
対合 の不動点,つまり
の不動点,つまり
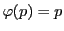 となる点を自己対合点という.
一つの対合について自己対合点は,
高々二個である.なぜならそれは2次同次方程式
となる点を自己対合点という.
一つの対合について自己対合点は,
高々二個である.なぜならそれは2次同次方程式
の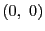 でない根でなければならないからである.
でない根でなければならないからである.
注意 3.3.2
ここで同次方程式とは,
未知数
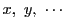
に関するいくつかの等式を連立したもので,
各等式は同次の等式であるもののことである.
これによって,解がある場合は未知数間の比が定まる.
同様にして次のことも成り立つ.
系 72.2
対合は,
- 対合をなすべき2組の点対
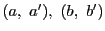 ,
,
- 対合をなすべき1組の点対
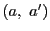 と一つの不動点,
と一つの不動点,
- 二つの不動点,
のいずれかを指定すれば一意に定まる.■
調和点列と対合に関する基本事項は次の命題である.
命題 73
直線
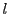
上の点の対合に関して次のことが成り立つ.
(1)
自己対合点が2個あるとき,
これらはその対合で対合をなす異なる2点を調和に分ける.
(2)
2定点を調和に分ける点対は,
2定点をその対合の自己対合点となす対合に関して,対合をなす.
(3)
点対
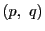
が2組の点対
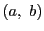
,
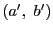
を同時に調和に分ければ,
点対
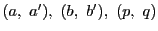
は対合をなす.
■
証明
(1)
2点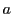 と
と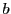 が対合をなすとし,
が対合をなすとし,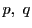 が自己対合点とする.
言いかえるとある射影変換
が自己対合点とする.
言いかえるとある射影変換 で
で
となるものがある.
複比は射影変換で不変であるから
同一の点はないので
![$\bigl[a,\ b;\ p,\ q\bigr]\ne 1$](images/img1967.gif) .
よって
.
よって
![$\bigl[a,\ b;\ p,\ q\bigr]=-1$](images/img1968.gif) .
.
直接計算
対合の行列を
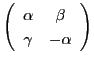 とする.
2点
とする.
2点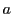 と
と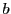 が対合をなすとし,
が対合をなすとし,
とおく.また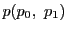 ,
,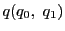 が自己対合点とする.
これらは2次同次方程式
が自己対合点とする.
これらは2次同次方程式
の根である.根と係数の関係から
である.
4点の複比は
である.ここで
各係数を根と係数の関係で整理すると
となる.分母は と
と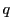 を入れ替えたものであり,
このとき
を入れ替えたものであり,
このとき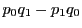 は符号だけが逆になる.
よって
は符号だけが逆になる.
よって
![$\bigl[a,\ b;\ p,\ q\bigr]=-1$](images/img1968.gif) であり,
自己対合点
であり,
自己対合点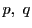 は対合をなす2点
は対合をなす2点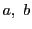 を調和に分ける.
を調和に分ける.
(2)
2定点
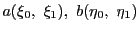 を
2点
を
2点
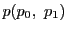 ,
,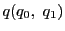 が調和に分けるとする.
が調和に分けるとする.
分母を払うと
これを整理すると
の形になる.よって命題72より
として行列
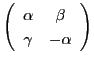 で定まる対合によって,2点
で定まる対合によって,2点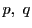 は対合をなす.
また
は対合をなす.
また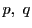 の両方に
の両方に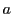 を代入しても,
を代入しても,
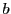 を代入しても方程式は満たされる.
つまり
を代入しても方程式は満たされる.
つまり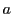 と
と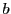 はこの対合に関する自己対合点である.
はこの対合に関する自己対合点である.
(3)
である.また
![$[a',\ b';\ q,\ p]=[a',\ b';\ p,\ q]^{-1}=-1$](images/img1982.gif) なので,
なので,
系72.1より,点対
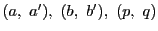 は対合をなす.
□
は対合をなす.
□
対合に関する古典的命題は数多くある.
ここではもっとも基本的なもののみ取りあげた.
これらの命題には古典的な射影幾何的証明と座標系による証明と,2系統の証明がある.
射影幾何の公理系から出発して座標系に至った立場では,
これは同等なのであるが,両方を試みるとたいへんおもしろく,
今後とも必要に応じて両方法の対比を考えることにする.


 次: 二次曲面
上: 射影変換と複比
前: 射影空間での複比
2014-01-03
次: 二次曲面
上: 射影変換と複比
前: 射影空間での複比
2014-01-03
 命題 70
完全四角形
命題 70
完全四角形
![]() が四角性六点であることを意味し,
直線体
が四角性六点であることを意味し,
直線体![]() の点における和の定義21から
の点における和の定義21から![]() を意味する.
同型
を意味する.
同型
![]() で
で
![]() なので,
なので,![]() .つまり
.つまり
![]() である.
□
である.
□![\begin{eqnarray*}[p_1\ p_3;\ e,\ c]
&=&[p_2\vee p_1,\ p_2\vee p_3;\ p_2\vee e,\...
...vee a,\ p_2\vee b;\ p_2\vee c,\ p_2\vee d]
=[a,\ b;\ c,\ d]=-1
\end{eqnarray*}](images/img1924.gif)
![]() 上の点
上の点![]() に対し,対合
に対し,対合![]() で
で
![]() 上に同次座標
上に同次座標![]() を設定する.
を設定する.
![]() を対合とする.可換体であるから,
を対合とする.可換体であるから,![]() は
線型写像
は
線型写像
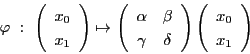
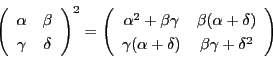
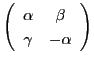 という形をしていて,
その行列式について
という形をしていて,
その行列式について
![]() 上の射影変換で考えるものとし,
さらに同次座標が設定されているものとする.
上の射影変換で考えるものとし,
さらに同次座標が設定されているものとする.
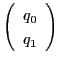 と
と
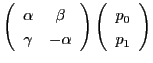 が同一の点となることである.よって
が同一の点となることである.よって
![]() に対応する行列を
に対応する行列を
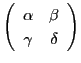 とおく.
点
とおく.
点![]() の非同次座標も
の非同次座標も![]() で表す.
条件から
で表す.
条件から
![]() の不動点,つまり
の不動点,つまり
![]() となる点を自己対合点という.
一つの対合について自己対合点は,
高々二個である.なぜならそれは2次同次方程式
となる点を自己対合点という.
一つの対合について自己対合点は,
高々二個である.なぜならそれは2次同次方程式
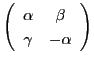 とする.
2点
とする.
2点![]() と
と![]() が対合をなすとし,
が対合をなすとし,
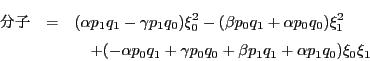
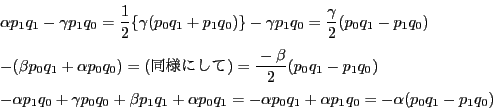
![]() を
2点
を
2点
![]() ,
,![]() が調和に分けるとする.
が調和に分けるとする.
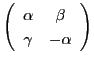 で定まる対合によって,2点
で定まる対合によって,2点