 点
点でも曲線の長さはどのように決めるのですか.
南海 一気に難しいところだ.
 点
点![]() から点
から点![]() までの連続でなめらかな曲線
までの連続でなめらかな曲線![]() の長さ
の長さ![]() は,次のように考える.
は,次のように考える.
曲線![]() 上に点列
上に点列
美樹 いろんな点列を考えるのですか.
南海
そう.
一つの点列![]() に対して
折れ線
に対して
折れ線
![]() の長さを
の長さを
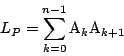
美樹
![]() も増やし
も増やし![]() をどんどん細かくしていった極限が曲線の長さなのですね.
をどんどん細かくしていった極限が曲線の長さなのですね.
南海
連続曲線に関していえばそのように考えてよい.
あらゆる折れ線![]() を考え,すべての
を考え,すべての![]() に関して
に関して
美樹
2点を結ぶ最小値が直線の長さなのだから,
分割を細かくすれば,和![]() は増大していく.
は増大していく.
曲線がはじめから折れ線でないかぎり,
折れ線での近似は近似であって![]() とは一致しない.
とは一致しない.
つねに![]() よりは小さい.
だからこんな言い方をするのですか.
よりは小さい.
だからこんな言い方をするのですか.
南海 そういうことだ. 詳しくは大学の解析で習ってもらいたい.
最近,これが数学IIIで必修でなくなったそうだ. 「計量」ということを高校数学に取り入れながら, 曲線の長さを外すというのは困ったことだ.
![]() 平面上の曲線
平面上の曲線![]() が,
が,
![]() と媒介変数
と媒介変数![]() によって表されているとする.
によって表されているとする.
![]() はそれぞれ
はそれぞれ![]() で微分可能とする.
で微分可能とする.
このとき,曲線![]() の
の
![]() に対応する
に対応する![]() 上の点
上の点![]() から
から
![]() に対応する
に対応する![]() 上の点
上の点![]() までの
長さ
までの
長さ![]() は
は
証明の概略を示そう.
![]() の区間
の区間![]() を
を![]() 等分し
等分し
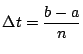 とおく.
とおく.
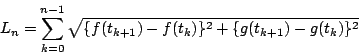
平均値の定理によって
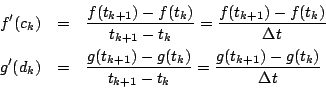
これから
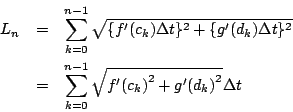
美樹 区分求積の形です.
南海 詳しくは『数学対話』−『定積分の定義』を見てほしい.
![]() と
と![]() と出てくるのでもう少し詳しく考えなければならないのだが,
と出てくるのでもう少し詳しく考えなければならないのだが,
![]() の極限が存在し,
の極限が存在し,
美樹
この値を![]() とするのですね.
とするのですね.
南海 高校の教科書では, 曲線の長さをすでに知っているものとして,次のように示す.
![]() に対応する
に対応する![]() 上の点
上の点![]() から
から
![]() に対応する
に対応する![]() 上の点
上の点![]() までの
長さを
までの
長さを![]() とおく.
とおく.
図のように![]() を
を![]() まで変化させる.
まで変化させる.![]() が小さいときは
曲線の長さの増加分
が小さいときは
曲線の長さの増加分
![]() は,
は,
証明を厳格にする方法はもちろんあるが,「ほぼ等しい」というつかみ方も大切だ.
よって
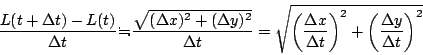
![]() の極限でこれは一致する.
の極限でこれは一致する.
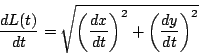

これから原始関数を求める計算をし,![]() を用いれば
を用いれば
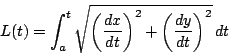
また曲線が![]() で表されるときは,
で表されるときは,![]() となるので,
となるので,
![]() を
を![]() に置きかえることで,
に置きかえることで,![]() の点から
の点から![]() の点までの長さ
の点までの長さ![]() は
は