角という量

南海　角もまた量である．この量をどのように量るか．

美樹　度で表す度数法と，ラジアンを単位とする弧度法があります．

南海　三角関数は歴史的には三角比からはじまった．三角形の内角を考えるかぎりは， $0^{\circ}$ から $180^{\circ}$ の範囲で考えていればよかった．

一方，角を円周上を動点がどれだけ動いたかを表すことに使おうとすると，何周でも回れるのだから $180^{\circ}$ では足りず，いくらでも大きい値がいるし，逆回りも考えれば負の値もいる．

こうして角は，すべての実数で定義されねばならなくなった．このように任意の実数値で考えた角を一般角という．

ところで，度数法は，1周の角を $360^{\circ}$ とするように，人間の歴史や習慣から決められたもので数学的な必然性はない．

円弧の長さをもって角度の値とする新しい方法を用いる．それが弧度法というもので，合理的で自然な定義である．

弧度法とは次のようにして角度という量の値を，円弧の長さでもって表す方法である．
平面上に原点 $\mathrm{O}$ を中心とする半径1の円をとる． $\mathrm{A}(1,\ 0)$ とする．

はじめ点 $\mathrm{A}$ の位置にあった動点 $\mathrm{P}$ が，円周上を反時計回り(左回り)にまわったとき， $\mathrm{P}$ が動いた長さをもって，対応する角 $\theta$ の値とする．

動点 $\mathrm{P}$ が，円周上を時計回り(右回り)にまわったとき， $\mathrm{P}$ が動いた長さに対し，その符号を負にした値をもって，対応する角 $\theta$ の値とする．

逆に，任意の実数値に対し，それが正なら，反時計回りに弧長がその値になるように点 $\mathrm{P}$ を動かしたときに定まる左回りの角をとり，それが負なら，時計回りに弧長がその値となるように点 $\mathrm{P}$ を動かしたときに定まる右回りの角をとる．

このようにすることで，任意の実数値に対して角が定まる．

弧度法の単位はラジアンである． 1ラジアンは，半径1の円の円弧の長さが1となる角で，度数法では約 $57.28^{\circ}$ に相当する.

普通は何もつけず 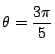$\theta=\dfrac{3\pi}{5}$ のように用いる．

美樹　 $\angle \mathrm{AOB}$ のように用いる記号「 $\angle$ 」は方向を考えていないように思います

南海　そうなのだ． $\angle$ は角の絶対値を表す．だから負の値はとらない．

それに対し，角は向きがあるので，同じ $\angle \mathrm{AOB}=\theta$ であっても，反時計回りにとるときは $+\theta$ ，時計回りにとるときは $-\theta$ とするのである．

Aozora Gakuen