次：弧長と三角関数　上: 計量ということ 前: 三角関数

余弦定理と正弦定理

美樹　 こうしてみると，余弦定理と加法定理が基礎なのですね． 正弦定理はどのような位置にあるのでしょうか．

南海　 正弦定理は余弦定理から導くことができる．

美樹　 余弦定理と正弦定理は別々の定理のように習います．

南海　 $\bigtriangleup \mathrm{ABC}$があり， 各頂点の対辺の長さを$a,\ b,\ c$とする．

$$\begin{eqnarray*} &&\cos A=\dfrac{b^2+c^2-a^2}{2bc},\ \\ &&\cos B=\dfrac{c^2+a^2-b^2}{2ca},\ \\ &&\cos C=\dfrac{a^2+b^2-c^2}{2ab} \end{eqnarray*}$$

が成り立つ．

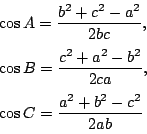
正弦定理とは，外接円の半径を$R$とするとき，

$$\dfrac{a}{\sin A}= \dfrac{b}{\sin B}= \dfrac{c}{\sin C}=2R$$

が成り立つことをいうものだ．

ところで三角形の内角なので，$\sin$はすべて正だから

美樹　 平方したものを比べればよい．

$$\begin{eqnarray*} &&\dfrac{a}{\sin A}=\dfrac{b}{\sin B}\\ &\iff&\dfrac{a^2}{\si... ...\iff&(a+b-c)(-a+b+c)(a+b+c)(a-b+c)=(a+b-c)(a-b+c)(a+b+c)(-a+b+c) \end{eqnarray*}$$

これは成立する．

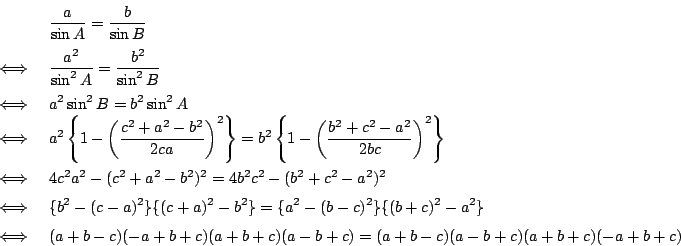
これで同様にして

$$\dfrac{a}{\sin A}= \dfrac{b}{\sin B}= \dfrac{c}{\sin C}$$

まで示せました．

この式の値が外接円の直径であることを示せば，正弦定理が示せます．

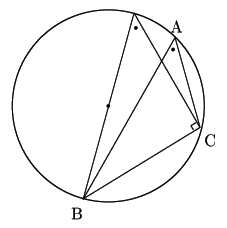
南海　 3つの角のうちどれかは鋭角だ． $A$が鋭角であるとして，2点 $\mathrm{B},\ \mathrm{C}$を 固定したまま，点$\mathrm{A}$を外接円周上を動かす．

美樹　 わかりました．このように点$\mathrm{A}$を動かしても， $\dfrac{a}{\sin A}$の値は不変です．

ですから，$\mathrm{BA}$が直径になるときを考えると，

$$2R\sin A=a$$

がわかります．