上: 計量ということ 前: 余弦定理と正弦定理

弧長と三角関数

美樹　角を円弧の長さで定義しました． 一方$y=f(x)$の曲線の長さもわかりました．

すると次の関係が成りたつはずです．

円の方程式は $y=\sqrt{1-x^2}$です．

$$y'=\dfrac{-2x}{2\sqrt{1-x^2}}=\dfrac{-x}{\sqrt{1-x^2}}$$

より

$$1+{y'}^2=1+\dfrac{x^2}{1-x^2}=\dfrac{1}{1-x^2}$$

ですから角$\theta$に対応する弧長が$\theta$になるので

$$\theta=\int_{\cos\theta}^1\sqrt{1+{y'}^2}\,dx= \int_{\cos\theta}^1\dfrac{1}{\sqrt{1-x^2}}\,dx$$

$y$方向に積分するのも同じなので

$$\theta=\int_0^{\sin\theta}\dfrac{1}{\sqrt{1-y^2}}\,dy$$

も成りたつはずです．

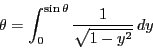
南海　その通りである．

積分変数を$t$にそろえ，$\cos\theta=x$とおくと， $\theta=\cos^{-1}x$と逆関数で表される．$\sin$も同様である． つまり

$$\begin{eqnarray*} \sin^{-1}x&=&\int_0^x\dfrac{1}{\sqrt{1-t^2}}\,dt\\ \cos^{-1}x&=&\int_x^1\dfrac{1}{\sqrt{1-t^2}}\,dt \end{eqnarray*}$$

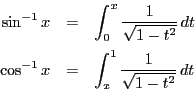
これは積分による三角関数の逆関数の定義である． 弧長による三角関数の定義という考え方は，現代数学に通じる新しい数学が18世紀から19世紀にはじまる一つの入り口だった．

美樹　三角関数の定義は一つではないのですね．

そうか． 『数学対話』『関数の展開とオイラーの公式』に 三角関数を級数で定義することが書かれていました．

南海　 そこでは三角関数を

$$e^{ix}=\cos x+i\sin x$$

として，つまり$e^{ix}$の実数部分と虚数部分として定めている．そこでは加法定理の別の証明を与えている．例1.2.1を見てほしい．この先は新しい世界だ．