南海 座標に極座標というのがあった.複素数平面上の点を極座標で表すことができる. つまり 直交座標で
史織 複素平面といったり複素数平面といったりしますが.
南海 もともとは複素平面だ.数年前に高校教科書に複素平面が登場したとき, これを「複素数平面」といったのだ.今も大学教科書は複素平面だ.だからどちらでもよい. 私は複素平面だ.
とにかくこれによって,平面図形を複素数で考えることができるようになる.
南海
座標に極座標というのがあった.複素数平面上の点を極座標で表すことができる.
つまり 直交座標で![]() となる点が極座標では
となる点が極座標では ![]() であったとする.
すると2つの座標の間には
であったとする.
すると2つの座標の間には
![]() が成り立つのだった.
が成り立つのだった.
これに応じて,複素数はさらに極形式という表し方がある.
![]() のとき
のとき
「形式」というのは「形」でのことで,同じ複素数 ![]() が,
が,
![]() と
と
![]() という2つの形をもつ.
極座標の
という2つの形をもつ.
極座標の ![]() は任意の実数でよいのだが,極形式のときには
は任意の実数でよいのだが,極形式のときには ![]() でとるので
負にはしないようにするのが約束である.
また,角
でとるので
負にはしないようにするのが約束である.
また,角 ![]() は
は ![]() 軸の正の方向から反時計回りに計る.
角
軸の正の方向から反時計回りに計る.
角 ![]() は偏角とよばれ
は偏角とよばれ ![]() と書く.
と書く.
ところがこの「極形式」は単に複素数のもう一つの表し方というだけではない. 三角関数の加法定理と複素数の積が対応するのだ.
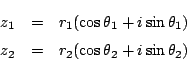
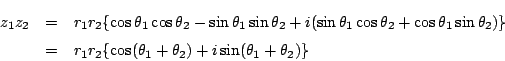
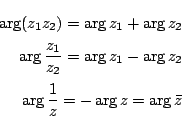
そこで
定理 5
ド・モアブルの定理
任意の整数 ![]() に対して
に対して
史織
証明
![]() のとき.数学的帰納法で示す.
のとき.数学的帰納法で示す.
![]() のときは両辺1であるから成立する.
のときは両辺1であるから成立する.
![]() で成立するとして,
で成立するとして,![]() で成立することを示す.
で成立することを示す.
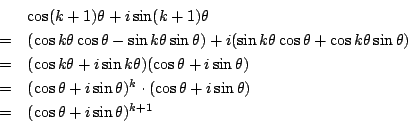
次に, ![]() のとき
のとき
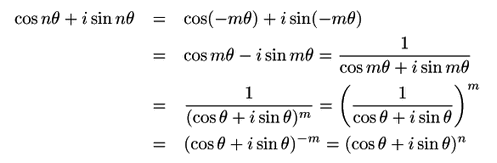
南海 この背景には人類が発見したもっとも美しい数学の公式「オイラーの公式」がある.
これらの背景と本質が知りたければ「オイラーの公式」を見てほしい.
2003年からまた複素数平面が高校数学から消える. 2012年に復活したが今度は行列が消える.このように消えたり復活したりするのは,日本の教育政策に理念がないからだ.
青空学園数学科は,高校時代に勉強するべき内容は長い歴史のなかで形成されるものであって, 国の教育政策で変えられるものではないと考えている. ド・モアブルの定理,複素数平面はまさに高校生が学ぶべき内容の一つである. 小学校の教育課程が世間の批判を受けてまた変わろうとしている. まったく右往左往しているのが今の文部科学省の姿だ. 複素数平面を高校数学に入れたり入れなかったりしているということは, 教育課程を決めている人がいかに高校数学に対してしっかりした見識をもっていないかを示している.
青空学園を訪れた高校生諸君は, 自分で「ド・モアブルの定理」までは理解するようにしてほしい.
史織
複素数で図形問題を考えるとき,すぐに ![]() と置いたり,
ベクトルのように考えるのです.
と置いたり,
ベクトルのように考えるのです.
複素数で図形を考える意味がよくわかりません.
南海 ベクトルなら成分に置くのではなく矢線で図形的に考えるのに,複素数ならすぐに成分で 書く人が確かに多い.
すでに ![]() で確認したように,複素数は加法,減法,実数倍を
考えるかぎりは,ベクトルとまったく同じである.
で確認したように,複素数は加法,減法,実数倍を
考えるかぎりは,ベクトルとまったく同じである.
2つの複素数 ![]() と
と ![]() が
が
![]() となる(つまり
となる(つまり
![]() が同じ直線上にない)とき,2つの実数
が同じ直線上にない)とき,2つの実数 ![]() に対して
に対して
だからこれらのことを考えるかぎり,ベクトルとして考えてかまわない.
しかし複素数で図形を考えるということは,複素数独自の方法を用いてこそ意味があるわけだ. だからすぐ成分表示したり,ベクトル的に考えると,複素数で図形を考える値打ちがない.
ベクトルと複素数の図形を考える上での違いがいくつかある.それをしっかり押さえてほしい.
いちばん大きい違いは,複素数には積があり,積を用いて回転が表せることである.
直線 ![]() を
を ![]() のまわりに角
のまわりに角 ![]() 回転した点を
回転した点を ![]() とすれば
とすれば
したがって直交することの処理もちがう.

つぎに絶対値,つまりは大きさの表し方が違う.
南海 さて,直交座標平面で直線の表し方は二つあった.
史織
一つは2点 ![]() と
と ![]() を通る直線は
を通る直線は
もう一つは,点 ![]() を通りベクトル
を通りベクトル ![]() に垂直な直線は
に垂直な直線は
南海 それと同じように,複素数による直線の表し方も二通りある.
![]() を動点とし,
を動点とし,
![]() などを
定点とする.また
などを
定点とする.また ![]() は原点である.
は原点である.
![]() が次の図形上にあるとき,
が次の図形上にあるとき, ![]() の満たすべき式を
の満たすべき式を
![]() などの複素数の(共役,絶対値などを用いた)等式で表わしてほしい.
まず第一の型に関するもの.
などの複素数の(共役,絶対値などを用いた)等式で表わしてほしい.
まず第一の型に関するもの.
例 1.4.2
史織
南海 大変よろしい.次は第二の型.
例 1.4.3
史織
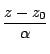 が純虚数.
が純虚数.
南海
最後のは,点
![]() を通り
を通り ![]() に直交することから
求めることもできる.
に直交することから
求めることもできる.
だから一般に
なぜならこの式を満たす任意の一点
![]() をとる.
をとる.
二式の辺々を引く.
つまり
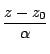 が純虚数.ゆえに,条件式を満たす
が純虚数.ゆえに,条件式を満たす 入試問題を紹介しておこう.
複素数平面において,原点を通らない直線の方程式は,0でない複素数 ![]() を用いて
を用いて
![]() と表すことができる.
と表すことができる.