1.
![]() に対して
に対して

ゆえに ![]() は体である.
は体である.
2.同様に乗法の逆元の存在を示せばよい.
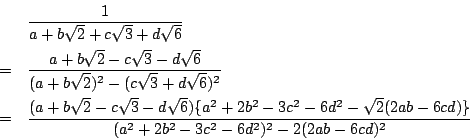
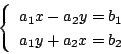
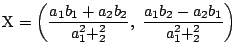 .また
.また
もし
![]() なら(1)から
なら(1)から
![]() となる.
一方
となる.
一方
![]() なので
なので
![]() となる以外にないが,このとき
となる以外にないが,このとき
![]() より
より
![]() となり相異なるという条件に反する.
となり相異なるという条件に反する.
ゆえに
![]() となり
となり
![]() つまり
つまり
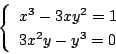
![]() なら
なら ![]() で
で
![]() となるので
となるので ![]() .
ゆえに
.
ゆえに ![]() .これを第1式に代入して
.これを第1式に代入して ![]() を得る.つまり
を得る.つまり
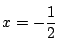 .これから
.これから
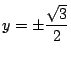 .
.
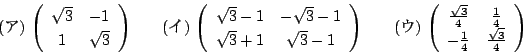
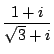 に対応する行列が
に対応する行列が 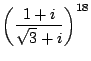 に対応する行列である.
に対応する行列である.
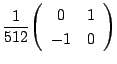
![]() 次式
次式 ![]() に対して
に対して![]() 個の
個の![]() に対する値が定まれば
に対する値が定まれば ![]() は一意に定まる.
実際
は一意に定まる.
実際
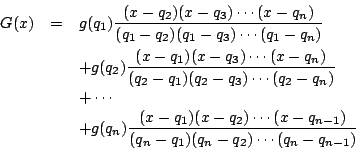
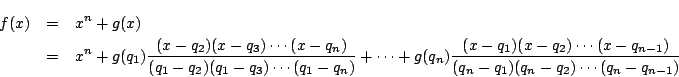
※これが「ラグランジュの補間公式」の方法である. つぎに数学的帰納法による解を示す.
![]() のとき.
のとき. ![]() とおく.
とおく.![]() で
で![]() が有理数なので,
が有理数なので, ![]() も有理数である.
も有理数である.
![]() のとき成立するとする.
のとき成立するとする.
![]() のとき.
のとき. ![]() を
を ![]() の係数が1である
の係数が1である ![]() の
の ![]() 次式とし,
相異なる
次式とし,
相異なる ![]() 個の有理数
個の有理数
![]() に対し
に対し
![]() がすべて有理数であるとする.
がすべて有理数であるとする.
因数定理より
![]() はすべて異なるので,
はすべて異なるので,
![]() に対し
に対し
数学的帰納法の仮定から ![]() は有理数係数の多項式である.ゆえに
は有理数係数の多項式である.ゆえに![]() から
から ![]() も
有理数係数の多項式である.
も
有理数係数の多項式である.
したがって題意が示された.
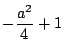
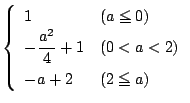
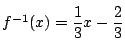 , 定義域:全実数
, 定義域:全実数
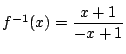 , 定義域:
, 定義域: 
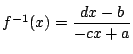 ,
定義域:
,
定義域:
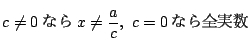
![\begin{eqnarray*}
f(x+1)-f(x)&=&a_n(x+1)^n-a_nx^n+[n-1以下の項のみ]\\
&=&a_n(nx^{n-1}+\cdots)+[n-1以下の項のみ]
\end{eqnarray*}](images/img1387.png)
十分条件であることを ![]() の次数
の次数 ![]() に関する帰納法で証明する.
に関する帰納法で証明する.
![]() のとき.
のとき. ![]() とおく.
とおく.
![]() について成立するとする.
について成立するとする.
![]() が整数で,階差がすべて整数なので,任意の整数
が整数で,階差がすべて整数なので,任意の整数![]() に対して
に対して![]() は整数値を取る.
は整数値を取る.
よって, 任意の次数 ![]() に関して『 』が示された.
に関して『 』が示された.
![]() のとき.
のとき. ![]() なので
なので
よって, 任意の ![]() に対して題意が成立した.
に対して題意が成立した.
任意の整数 ![]() に対して
に対して ![]() が整数なので
が整数なので
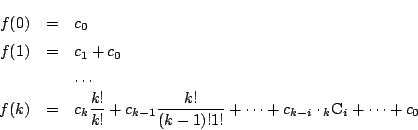
十分条件を示す.
![]() なら
なら
![]() のとき
のとき ![]() とすると
とすると
以上で必要十分条件であることが示された.
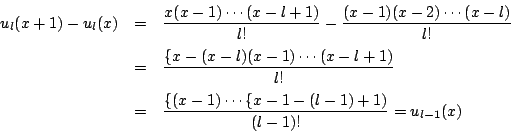
注意2
2の証明をよく見れば
1の条件: ![]() 連続整数で
連続整数で ![]() が整数値を取ること
が整数値を取ること
2の条件:
![]() がすべて整数であること
がすべて整数であること
の同値性を直接示すこともできる.
![]() とおき,有限和
とおき,有限和![]() を
を
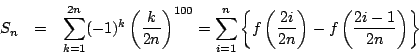
![]() のとき平均値の定理から
のとき平均値の定理から![]() で
で
![$\left[\dfrac{2i-1}{2n},\ \dfrac{2i}{2n} \right]$](images/img1435.png) に用いて,
に用いて,
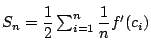 とリーマン和で表せた.
とリーマン和で表せた.
![\begin{displaymath}
\lim_{n \to \infty}\sum_{i=1}^nS_n=
\dfrac{1}{2}\int_0^1f'(x...
...right]_0^1
=\dfrac{1}{2}\left[x^{100} \right]_0^1=\dfrac{1}{2}
\end{displaymath}](images/img1438.png)
注意
この問題はどこまで一般化できるのか.
![]() が微分可能で
が微分可能で![]() が連続な任意の関数で次式が成立する.
が連続な任意の関数で次式が成立する.
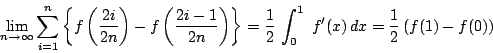
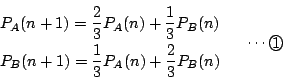
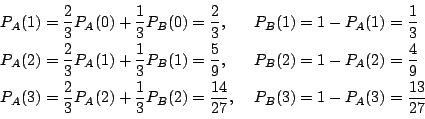
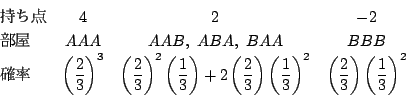
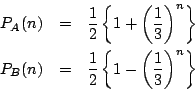
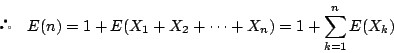
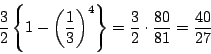
一方![]() となるのは,2つの目の出方が
となるのは,2つの目の出方が
![]() のとき.
のとき.
![]() を
を![]() に固定する.このとき2回目に出る目を
に固定する.このとき2回目に出る目を![]() とすれば
とすれば![]() となるのは
となるのは
一方![]() となるのは,1回目の結果が
となるのは,1回目の結果が
![]() のいずれに対しても,
2回目に出るべき目は
のいずれに対しても,
2回目に出るべき目は![]() を6で割った余りなのでただ一つである.
を6で割った余りなのでただ一つである.
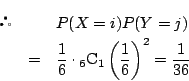
一方![]() となるのは,
となるのは,![]() が
が![]() のいずれに対しても,
2回目の目は
のいずれに対しても,
2回目の目は![]() を3で割った余りなので2つある.
を3で割った余りなので2つある.
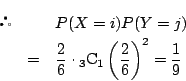
![]() のとき.
のとき.![]() となるのは,4の目が連続する場合なので
となるのは,4の目が連続する場合なので
一方![]() となるのは,2つの目の出方が
となるのは,2つの目の出方が
![]() のとき.
のとき.![]() のとき,
のとき,![]() となることはない.
となることはない.
一方![]() となるのは,2つの目の出方が
となるのは,2つの目の出方が
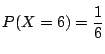 なので
なので
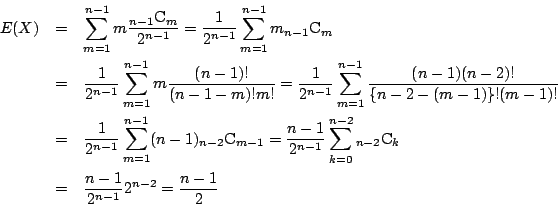
方法2
二項定理より
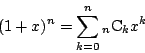
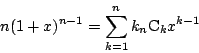
[(4)の別解]
確率変数![]() を
を
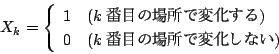
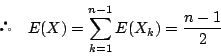

つまり
![]() が真となる
が真となる ![]() の条件は
の条件は