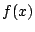 と
と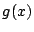 は同一の式である.つまり,
次数が等しくかつ同じ次数の項の係数が等しい.
は同一の式である.つまり,
次数が等しくかつ同じ次数の項の係数が等しい.
- 任意の
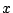 の値に対して
の値に対して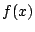 と
と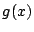 は同一の値をとる.
は同一の値をとる.
- 等式
 が互いに異なる
が互いに異なる 個の
個の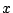 の値に対して成り立つ.
の値に対して成り立つ.
現在の教科書では,恒等式の定義を習った段階で,因数定理はまだである.そのため,次の大変重要な基本定理が高校数学から拔け落ちている.
証明
![]() が多項式関数でなければ,成り立つとはかぎらないことにも注意しよう.
が多項式関数でなければ,成り立つとはかぎらないことにも注意しよう.
史織
関数![]() で
で
![]() が成り立たない例.
が成り立たない例.
関数![]() で
で
![]() が成り立たない例.
が成り立たない例.
南海 その通り.一般に周期関数で反例が作れる.
史織
「 .つまり
.つまり ![]() 」と言うところはそれぞれ恒等式として成立ということですね.
」と言うところはそれぞれ恒等式として成立ということですね.
南海
その通り.整式![]() を整式
を整式 ![]() で割ったとき,商が
で割ったとき,商が ![]() で余りが
で余りが ![]() なら
なら
ところで,上の恒等式の基本性質によると,![]() 次の整式
次の整式 ![]() に対し,
に対し, ![]() の
の ![]() 個の値
個の値
史織
![]() と
と ![]() が同じ値になるとすると
が同じ値になるとすると
南海 その通り.
さて,となると次の問題が考えられる.
![]() 個の値
個の値
史織 『青空学園』で見ました.「ラグランジュの補間公式」です.

これは確かに
南海
それではもう一つ.次の今年の京大の問題を,数学的帰納法を用いないで,
ラグランジュの補間公式を用いて解け.
南海 この問題は数学的帰納法と方法を指定しない方がよかった.
とりあえず以上としよう.またわからないことがあれば質問してほしい.
史織 ありがとうございました.