南海 まず教科書はどのように書いているのかそれから見てみよう.
史織 教科書ではまず写像を定義し,その上で関数を定義しています.
二つの集合において,ある対応によって
とき,この対応をから
への写像といい記号
などを用いて
と書きあらわす.
写像において集合
を定義域という.
写像によって
の要素
に 対応する
の要素を
と書き,これを
による
の像,または
の
における値という.また値全体の集合
を 写像
の値域という.
定義域と値域が,ともに数の集合である写像を関数という.
南海 これが基本的な関数と写像に関する定義だ.
史織
関数を ![]() などと書きます.これはどういうことになるのでしょうか.
などと書きます.これはどういうことになるのでしょうか.
南海 ここで文字とは何であったかを思い起こそう.それは「数を入れる箱」だった.
史織
![]() では箱
では箱 ![]() に集合
に集合![]() の要素を入れると,それに対応して
の要素を入れると,それに対応して
![]() の要素が定まる.その値を入れる箱 が
の要素が定まる.その値を入れる箱 が ![]() です.
です.
南海
関数を考えるときに用いる箱としての文字のことを「変数」というのだった.
定義域側の変数を 独立変数 といいこれを普通 ![]() で表わし,
値域側の変数を従属変数 といいこれを普通
で表わし,
値域側の変数を従属変数 といいこれを普通 ![]() で表わすことが多い.
で表わすことが多い.
史織
![]() なら
なら ![]() に2を入れれば
に2を入れれば ![]() には4が入る.
「
には4が入る.
「 ![]() の
の ![]() における値が
における値が ![]() 」ということですね.
」ということですね.
南海
![]() における「等号」の意味もいま言った通りだ.つまり「その値を入れる箱 が
における「等号」の意味もいま言った通りだ.つまり「その値を入れる箱 が ![]() 」
ということを「
」
ということを「![]() 」で表すのだ.
」で表すのだ.
史織 日頃何となく使っている記号もしっかりとして意味があるのですね.
南海 その通り.あいまいなことは何もない.
関数についていくつかの注意を述べよう.
まず関数というのは,数から数への対応の規則なので,一つの式で表される必要はない.例えば,
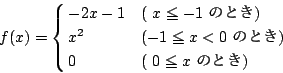
対応の規則 ![]() が
が ![]() の式で定められているときに,その式が
の式で定められているときに,その式が ![]() の
整式であるなら,その次数によって一次関数,二次関数,などと呼ぶ.
その式が整式のとき,整式関数(多項式関数,有理整関数)と呼ぶ.
また,その式が,
の
整式であるなら,その次数によって一次関数,二次関数,などと呼ぶ.
その式が整式のとき,整式関数(多項式関数,有理整関数)と呼ぶ.
また,その式が, ![]() の有理式のとき有理関数,無理式のとき無理関数,
さらに同様に三角関数,指数関数,対数関数,などと呼ぶ.
の有理式のとき有理関数,無理式のとき無理関数,
さらに同様に三角関数,指数関数,対数関数,などと呼ぶ.
その上で以下は二次関数を例にとって考えよう.二次関数とは対応の規則が二次多項式であるものだ.
つまり
![]() と表せる関数のことである.
と表せる関数のことである.
定義域が全実数の場合,
![]() に対する二次関数
に対する二次関数 ![]() の値域を,
の値域を,
![]() についての不等式で表すと次のようになる.
についての不等式で表すと次のようになる.
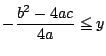 .
.
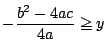 .
.
これは平方完成してもわかるが,微分法で考えてもよい.
![]() より,
より,
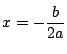 で極値
で極値
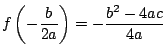 をとり,
をとり,
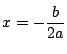 で極小かつ最小.
で極小かつ最小.
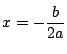 で極大かつ最大.
で極大かつ最大.
つぎに,定義域が
![]() の場合,二次関数
の場合,二次関数
![]() の値域はどのようになるのか.
の値域はどのようになるのか.
 史織
史織
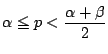 なら,
なら,
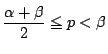 なら,
なら,
南海 グラフとは何かということは後で考えるとしてこれでよい. だから軸がどこにあるかで最大値や最小値がかわってくる. 軸による場合分けの練習問題を掲げておくのでやってみてほしい.
南海 関数の値域が確定すれば,関数の取る値の最大値と最小値が 確定する.しかし,逆に,次の例が示しているように, 関数の取る値の最大値と最小値が確定しても,その間のすべての値を 取るとはかぎらないので,値域は確定しない.
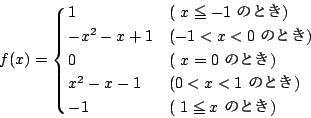
![]() のグラフをかき,値域,最大値
のグラフをかき,値域,最大値 ![]() ,最小値
,最小値 ![]() を求め,値域が
を求め,値域が ![]() とはならないことを確認してほしい.
とはならないことを確認してほしい.
このようにグラフが連続していない関数では,値域は必ずしも, 最大値と最小値の間のすべてをとるわけではない. このことに注意し,最大値,最小値問題でも,基本的には 値域を確定することによって,求めるようにしたい.
さらにもう一題.
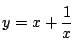 の値域を求めよ」
という問題に対し,A君の解答の一部を示す.
の値域を求めよ」
という問題に対し,A君の解答の一部を示す.
[解答]相乗平均,相加平均の関係をもちいると,
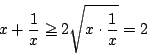
したがって,これについて以下の問に答えよ.において
.
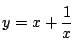 の微分を用いて値域を求めよ.
の微分を用いて値域を求めよ.
南海 これはどうだろうか.
史織 えっ.この解答でいいと思うのですが.
南海
だが,
例えば 定義域を![]() として関数
として関数
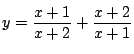 はどうか.
これも確かに
はどうか.
これも確かに
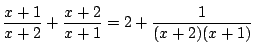 なので単調に減少し
値域は
なので単調に減少し
値域は
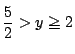 だ.
だ.
史織
そうか.
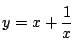 のばあいも2以上であることはまちがいないが,
2以上の値をすべてとることができるかどうかはわからないのですね.
のばあいも2以上であることはまちがいないが,
2以上の値をすべてとることができるかどうかはわからないのですね.
南海 相加相乗平均の関係の不等式は必要条件なのだ.上の問の続きをやってみてほしい.
史織 はい.
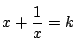 とおくと
とおくと ![]() となる.これが
となる.これが ![]() の解をもつ条件を求める.
2解の積は1で正なので条件は
の解をもつ条件を求める.
2解の積は1で正なので条件は
これは十分条件でもあるのですか.
南海
そう. ![]() が存在しうる範囲の必要十分条件が
が存在しうる範囲の必要十分条件が ![]() が存在することだからだ.
が存在することだからだ.
史織 これはいわゆる逆像法という方法ですね.
次に(3)の方法.
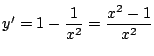 .したがって
.したがって ![]() で極小かつ最小でこのとき
最小値は2.
で極小かつ最小でこのとき
最小値は2.
![]() なので値域は
なので値域は![]() .
.
いつもはこんなに詳しくやっていません.
南海
本当はやらなくてはいけない. ![]() の関数
の関数 ![]() が整理すると
が整理すると
![]() で表され,
で表され,
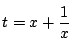 とおいて
とおいて ![]() の最大値や最小値を求める問題はよくある.
このとき
の最大値や最小値を求める問題はよくある.
このとき ![]() のとりうる値の範囲を求めなければならない.
のとりうる値の範囲を求めなければならない.
ところが参考書でも ![]() の値域をしっかり求めるのではなく,
相加相乗平均の関係の不等式で必要条件としての
の値域をしっかり求めるのではなく,
相加相乗平均の関係の不等式で必要条件としての ![]() の範囲だけで求めて,
その後最大や最小を与える
の範囲だけで求めて,
その後最大や最小を与える ![]() を実際に求めて存在を示しておくことで,済ましているものも多い.
それでよいときもあるが,ここは常に正確に考えるようにしよう.
を実際に求めて存在を示しておくことで,済ましているものも多い.
それでよいときもあるが,ここは常に正確に考えるようにしよう.