南海 確率の定義から次の余事象の確率,和事象の確率の公式も出てくる.
標本空間![]() の事象
の事象![]() に対して,
に対して,![]() の補集合で定まる事象を
の補集合で定まる事象を![]() と書き,
余事象という.
と書き,
余事象という.
また2つの事象![]() と
と![]() に対してその和集合と積集合によって定まる事象を和事象,積事象といい,
に対してその和集合と積集合によって定まる事象を和事象,積事象といい,
![]() ,
,![]() と書く.このとき
と書く.このとき
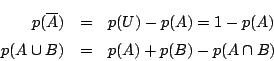
史織
証明してみます.
![]() で
で
![]() なので確率の定義(iii)から
なので確率の定義(iii)から
次に
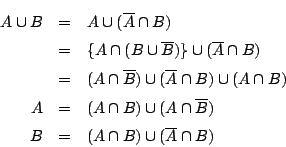
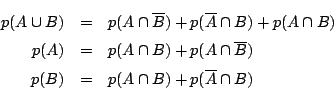
これから
南海
これでよい.教科書は,個数の公式
![]() のとき,事象
のとき,事象![]() と事象
と事象![]() は互いに排反であるという.
は互いに排反であるという.
史織 質問です. 確率を全ての事象に確率値を対応させる関数として定義しましたが, 事象はすべて根元事象の和集合になるので,根元事象の確率が定まっていれば, 一般の事象の確率はそれを構成する根元事象の確率の和になるのではないでしょうか. なぜ先のような定義をする必要があるのでしょうか.
南海
根元事象が有限個の場合はその通りなのだ.無限個あっても
![]() と数えられるような離散的
な場合も含めて,事象
と数えられるような離散的
な場合も含めて,事象![]() の確率
の確率![]() は
は
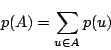
ところが連続的な確率の場合にはこれでは定義にならない. 例えば,ある人が6時から7時のいずれかの時刻に駅に着く.6時から7時のいずれかの時刻に着く確率も等しい. この場合,試行の結果は,着く時刻の全体である.
6時5分から10分の間に着く確率は何か.これは
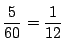 である.
しかし根元事象の確率,ちょうど6時3分に着く確率は0.厳密には測度というものが0なのだが,
いずれにしても根源事情の和にはならない.
である.
しかし根元事象の確率,ちょうど6時3分に着く確率は0.厳密には測度というものが0なのだが,
いずれにしても根源事情の和にはならない.
史織 わかりました.