確率変数![]() が互いに独立であるとは,
が互いに独立であるとは,![]() のとる任意の値
のとる任意の値![]() と
と![]() のとる任意の値
のとる任意の値![]() について
について
確率変数![]() と
と![]() が互いに独立であるときは,確率変数
が互いに独立であるときは,確率変数![]() の期待値は
の期待値は

史織
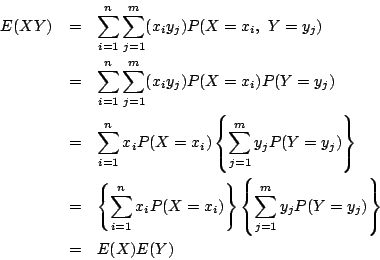
積についても,
期待値は根元事象の全体にわたる和であるという観点から
![]() を示せませんか.
を示せませんか.
南海 それは無理だ.どうしてかというと,事象の独立性が基本なのだが,根元事象は互いに独立ではないので, 根元事象に帰着させることは出来ない.
ここで確率変数の独立性を問う過去問題を紹介しよう.
正![]() 角形の頂点に
角形の頂点に
![]() と時計回りに番号がつけてある.頂点0を出発点とし,
サイコロを投げて出た目の数だけ頂点を時計まわりに移動し,着いた頂点の番号を
と時計回りに番号がつけてある.頂点0を出発点とし,
サイコロを投げて出た目の数だけ頂点を時計まわりに移動し,着いた頂点の番号を![]() とする.
次にもう一度サイコロを投げて出た目の数だけ,頂点
とする.
次にもう一度サイコロを投げて出た目の数だけ,頂点![]() から時計まわりに移動し,着いた頂点の番号を
から時計まわりに移動し,着いた頂点の番号を![]() とする.
このようにして定めた確率変数
とする.
このようにして定めた確率変数![]() について
について
ただし,確率変数![]() が互いに独立であるとは,
が互いに独立であるとは,
![]() となる確率
となる確率![]() と,
と,
![]() となる確率
となる確率![]() との間に,次の等式が任意の
との間に,次の等式が任意の
![]() について
成り立つことである.
について
成り立つことである.