南海 この節の後半は数学Cで習う範囲なのだが,数Aの確率の理解のためにもぜひ押さえておきたい.
確率空間![]() と2つの事象
と2つの事象![]() と
と![]() があるとする.
があるとする.
 確率
確率![]() に対して,事象
に対して,事象![]() が起こったという前提のもとで
が起こったという前提のもとで![]() が起こる確率
が起こる確率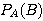 を考える.
を考える.
史織
事象![]() が起こったことが前提なので,
が起こったことが前提なので,![]() でなければならない.
事象
でなければならない.
事象![]() が起こったという前提のもとで
が起こったという前提のもとで![]() が起こるので,
が起こるので,![]() の部分集合として事象は
の部分集合として事象は![]() です.
この事象
です.
この事象![]() が事象
が事象![]() の確率を1としたとき,どのような確率で起こるかが
の確率を1としたとき,どのような確率で起こるかが
![]() だから,
だから,![]() とあわせて
とあわせて
南海
そういうことだ.![]() が起こるという条件の下での確率なので条件付き確率という.
が起こるという条件の下での確率なので条件付き確率という.
条件付き確率![]() は,集合
は,集合![]() を標本空間とする確率になっている.
を標本空間とする確率になっている.
つまり,標本空間![]() を狭めて,集合
を狭めて,集合![]() を新たな標本空間とし,
を新たな標本空間とし,
![]() に含まれる
に含まれる![]() の要素
の要素![]() の確率
の確率![]() を
を![]() となるように
となるように
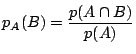 で定義する.このとき
で定義する.このとき![]() が新たな確率空間となる.
が新たな確率空間となる.
史織
確認してみます.確率の定義の条件をみたせばよいのですね.![]() に対しては
に対しては![]() で
で
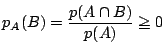
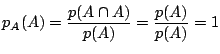
![]() や
や![]() が
が![]() の部分集合でなくても
の部分集合でなくても
![]() なら
なら
![]() なので
なので
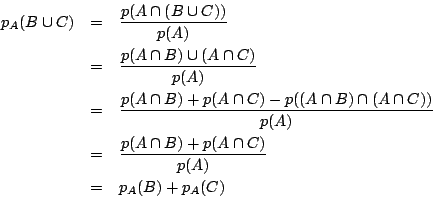
南海
それは
![]() で
で
![]() のときの証明の中で済んでいる.
しかしいろいろやってみることは大切だ.
のときの証明の中で済んでいる.
しかしいろいろやってみることは大切だ.
なお,根元事象が同様に確からしく,集合の要素の個数で確率が決まるときは,
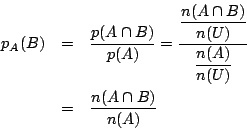
そこで大切なこと.