次： 命題と条件 上： 条件付確率 前： 条件付確率

事象の独立

確率空間$(U,\ p)$の2つの事象$A$と$B$に対して

$$p_A(B)=p(B)$$

が成り立つとき，事象$A$と$B$は互いに独立という．

根元事象が同様に確からしく，集合の要素の個数で確率が決まるときは，図のように

$$\dfrac{n(A\cap B)}{n(A)}=\dfrac{n(B)}{n(U)}$$

となると言うことだ．

 

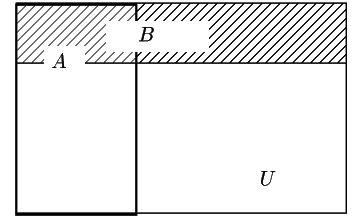
史織　 まったく互いに影響しあわない2つの試行は独立で， それぞれのある結果が同時に起こる確率はそれぞれが起こる確率の積である， と数Aの教科書には書かれています． これは条件付き確率を用いてどのように表されるのでしょうか．

南海　 2つの確率空間$(U_1,\ p_1)$と$(U_2,\ p_2)$があるとしよう． $p_1$は$U_1$だけで，$p_2$は$U_2$だけで定まっているとする．

今の質問を一般的に説明するのはなかなか難しいのだ． 具体的には結果の総数が有限である場合は簡明なので， この場合について説明していこう．

$$\begin{eqnarray*} U_1&=&\{u_1,\ u_2,\ \cdots,\ u_s\}\\ U_2&=&\{v_1,\ v_2,\ \cdots,\ v_t\} \end{eqnarray*}$$

があって， $u=u_1,\ u_2,\ \cdots,\ u_s$と $v=v_1,\ v_2,\ \cdots,\ v_t$に対して 確率$p_1(u)$と$p_2(v)$が定まっているとする． $p_1$と$p_2$はそれぞれ$U_1$と$U_2$の事象だけで定まり， たがいに$U_2$と$U_1$の事象とは無関係であることに注意しよう．

新たな標本空間$U$を

$$U=\{(u,\ v)\ \vert\ u\in U_1,\ v\in U_2\}$$

で定め，この標本空間に確率$q$を

$$q\{(u,\ v)\}=p_1(u)\cdot p_2(v)$$

で定める．集合$U$を$(U_1,\ U_2)$のように書こう．

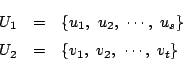
同様に$U_1,\ U_2$のそれぞれの部分集合$A,\ B$に対して， $U=(U_1,\ U_2)$の部分集合

$$\{(u,\ v)\ \vert\ u\in A,\ v\in B\}$$

を$(A,\ B)$のように書こう．

同時に2つの試行を行うときに，$U_1$の事象$A$が起こるとは， $U_2$の方は何が起こってもよいのだから，$U$の事象$A$を

$$(A,\ U_2)=\{(u,\ v)\ \vert\ u\in A,\ v\in U_2\}$$

で定めれば，これは$A$と同一視できる．$A$の$U$への埋め込みと言おう． 同様に$U_2$の事象$B$に対して$(U_1,\ B)$で，$B$を$U$に埋め込む．

任意の$U_1$の事象$A$と$U_2$の事象$B$に対して， このようにして埋め込まれた$U$の事象$(A,\ U_2)$と$(U_1,\ B)$は互いに独立である．

史織　 証明してみます．

$$(A,\ U_2)\cap (U_1,\ B)=(A,\ B)$$

なので

$$\begin{eqnarray*} q\{(A,\ U_2)\}&=&\sum_{u \in A,\ v \in U_2} p_1(u)p_2(v)\\ &=... ...v \in B} p_2(v)\right\}=\sum_{u \in A} p_1(u)p_2(B)=p_1(A)p_2(B) \end{eqnarray*}$$

より

$$q_{(A,\ U_2)}\{(A,\ U_2)\cap (U_1,\ B)\}=\dfrac{p_1(A)p_2(B)}{p_1(A)}=p_2(B)$$

一方

$$\begin{eqnarray*} q\{(U_1,\ B)\}&=&\sum_{u \in U_1,\ v \in B} p_1(u)p_2(v)\\ &=... ...n U_1} p_1(u)\right\}\left\{\sum_{v \in B} p_2(v)\right\}=p_2(B) \end{eqnarray*}$$

なので，確かに

$$q_{(A,\ U_2)}\{(A,\ U_2)\cap (U_1,\ B)\}=q\{(U_1,\ B)\}$$

が任意の$A$と$B$について成立する．

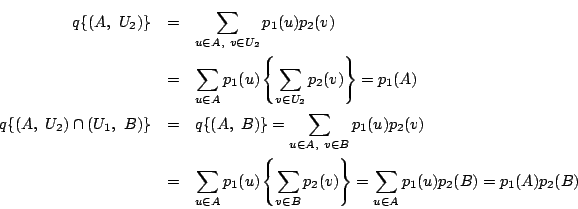
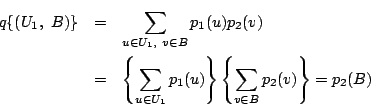
南海　 そういうことだ．