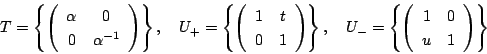次: 微分作用素
上: 方程式の不変式
前: 判別式だけか
南海
そういうことだ.
まず,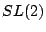 の任意の要素は,3つの型の行列
の任意の要素は,3つの型の行列
の積に分解することが出来る.
耕介
やってみます.
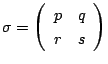 をとります.
をとります.
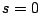 のときは
のときは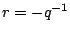 なので
なので
です.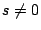 のときは
のときは
です.
南海
そこで,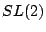 の部分集合を次のように定める.
の部分集合を次のように定める.
これらはいずれも積で閉じている.単位行列,逆行列も同じ形をしている.
つまり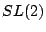 の部分群である.
そして,
の部分群である.
そして,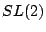 はこれら3つの部分群で生成される.
つまり,これらの3つの部分群の要素をさまざまにかけあわせれば,
はこれら3つの部分群で生成される.
つまり,これらの3つの部分群の要素をさまざまにかけあわせれば,
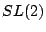 の要素がすべて得られる.
の要素がすべて得られる.
耕介
すると,2次方程式の不変式を考える場合,
これら3つの型の行列について不変であればいいのですね.
この方に対応する3次行列(6)
を書いてみます.
これらに対応する変換(6)
で不変なものを確定すればよいということになります.
Aozora Gakuen
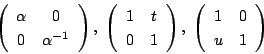
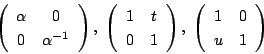
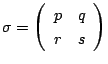 をとります.
をとります.
![]() のときは
のときは![]() なので
なので
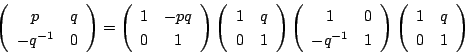
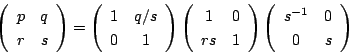
![]() の部分集合を次のように定める.
の部分集合を次のように定める.