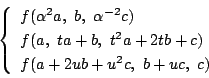
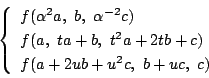
南海
これらの変換は![]() の1次式で定まるので,
単項式
の1次式で定まるので,
単項式![]() の次数
の次数![]() を変えない.
だから
を変えない.
だから![]() がこれらの変換で不変なら,
その同次数の項を集めた部分が不変である.
だからはじめから
がこれらの変換で不変なら,
その同次数の項を集めた部分が不変である.
だからはじめから![]() は3変数の同次式であるとしてよい.
は3変数の同次式であるとしてよい.
![]() は
単項式
は
単項式![]() を単項式
を単項式
![]() に変える.
に変える.
![]() が
が![]() の整式として恒等的に
の整式として恒等的に![]() と等しいのなら,
各単項式の係数が一致しなければならない.
したがって
と等しいのなら,
各単項式の係数が一致しなければならない.
したがって
![]() .
つまり
.
つまり![]() である.
よってこの変換
である.
よってこの変換
![]() で不変な同次式は,
で不変な同次式は,
![]() という形をした次数の等しい単項類からなることが必要である.
つまり,不変式は
という形をした次数の等しい単項類からなることが必要である.
つまり,不変式は![]() と
と![]() で対称である.
で対称である.
したがって
群![]() と
と![]() で不変なら,必然的に
で不変なら,必然的に![]() でも不変である.
もちろん
群
でも不変である.
もちろん
群![]() と
と![]() で不変なら,必然的に
で不変なら,必然的に![]() でも不変である.
といってもよい.
でも不変である.
といってもよい.
耕介
少しずつわかってきました.
![]() が
が![]() のこの作用で不変であるためには
変数
のこの作用で不変であるためには
変数![]() と
と![]() は必ず
は必ず![]() という形で入っていなければならない.
だから
という形で入っていなければならない.
だから![]() か
か![]() で不変であればよい.
で不変であればよい.
ところで,
![]() が
任意の
が
任意の![]() で
で![]() に等しいということは,
に等しいということは,
![]() を
を![]() で微分した
導関数が0,つまり文字係数
で微分した
導関数が0,つまり文字係数![]() をもつ
をもつ![]() の整式として
の整式として
南海 いいところに気がついた.
耕介 この微分は合成関数の微分ですが, 変数が3個あるので難しいです.
南海
![]() 3変数の関数
3変数の関数![]() を
その中の
を
その中の![]() について微分することを
について微分することを
![]() と書く.
と書く.
耕介
![]() の項
の項
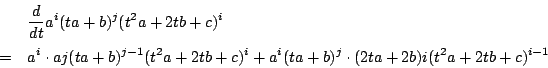
 によって変換した
によって変換した
南海
任意の![]() で0になるのだから
で0になるのだから![]() でも0になることが必要.
これから恒等的に
でも0になることが必要.
これから恒等的に
注意
先に注意したように![]() と
と![]() について対称なので次の条件でもよい.
について対称なので次の条件でもよい.
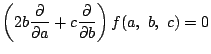
かっこ内の微分の組合せは, 3変数の関数に作用するので微分作用素という. これらの微分作用素を次のように置く.
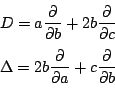
耕介
これは何にせよ,
![]() 3変数の整式を同じ3変数の整式に写します.
つまり
3変数の整式を同じ3変数の整式に写します.
つまり![]() の要素を同じ
の要素を同じ![]() に写します.
に写します.
南海
さらに2つの整式
![]() ,
および数定数
,
および数定数![]() に対して
に対して
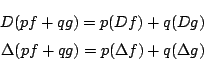
耕介 ベクトル空間の線型写像のようです.
南海 まさにそうだ.