耕介
定理6の条件(i)を満たすもののなかで,
![]() の作用で0になるのもを考えればいいのですね.
つまり
の作用で0になるのもを考えればいいのですね.
つまり![]() と
と![]() の次数が等しいもののなかで考えればよい.
の次数が等しいもののなかで考えればよい.
南海
![]() がどのような作用であるかを見るために
次数が
がどのような作用であるかを見るために
次数が![]() の単項式
の単項式
耕介
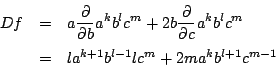
南海
いずれの項も![]() の指数と
の指数と![]() の指数との差が1増え,
それに応じて,
の指数との差が1増え,
それに応じて,
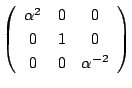 の作用によって
の作用によって![]() の指数は2増加する.
そこで,
の指数は2増加する.
そこで,![]() の整式で,それを構成する各単項式が
指数が
の整式で,それを構成する各単項式が
指数が![]() で,
で,![]() の指数と
の指数と![]() の指数との差の2倍を
の指数との差の2倍を![]() とし,
とし,
![]() とおこう.
これらはこの条件を満たす単項式を基底とする
とおこう.
これらはこの条件を満たす単項式を基底とする![]() 上のベクトル空間だ.
上のベクトル空間だ.
![]() と
と![]() に属する単項式をあげてみてほしい
に属する単項式をあげてみてほしい
耕介
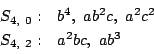
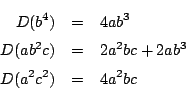
![]() 上のベクトル空間としては
上のベクトル空間としては
![]() は3次元,
は3次元,![]() は2次元です.
は2次元です.
![]() や
や![]() はこのようなベクトル空間の線型写像になっているのですね.
はこのようなベクトル空間の線型写像になっているのですね.
南海
そうだ.しかも上の基底の変換からわかるように,
![]() は
は![]() から
から![]() の上への線型写像だ.
の上への線型写像だ.
すると,![]() の部分空間で
の部分空間で![]() の作用によって0になるものの
作る空間の次元はいくらか.
の作用によって0になるものの
作る空間の次元はいくらか.
耕介 3次元から2次元に射影するのだから, それで0になる部分空間は1次元です.
ということは![]() の整式で,今考えている変換で不変で,
4次であるものは,基底が1個,つまりひとつの整式で表される.
の整式で,今考えている変換で不変で,
4次であるものは,基底が1個,つまりひとつの整式で表される.
ということはその基底は![]() の定数倍のみ.
の定数倍のみ.
同様にして, 2次方程式の不変式は判別式とそのべきしかないことが示せそうです.
南海 問題を整理しよう.
![]() の要素が不変式であるということは,
定理6の2つの条件を満たすということである.
条件(i)を満たすことはある
の要素が不変式であるということは,
定理6の2つの条件を満たすということである.
条件(i)を満たすことはある![]() に関する
に関する![]() の要素であるということだ.
の要素であるということだ.
次に微分作用素![]() は
は
![]() から
から![]() での線型写像である.
での線型写像である.
そこで,
![]() と
と![]() の次元を調べ,
さらに
の次元を調べ,
さらに![]() が上への写像であることとを確認して,
が上への写像であることとを確認して,
![]() の次元を確定させよう.
の次元を確定させよう.
耕介
![]() の次元は,
の次元は,
![]() となる0以上の整数の組
となる0以上の整数の組![]() の個数です.
また,
の個数です.
また,![]() の次元は,
の次元は,
![]() となる0以上の整数の組
となる0以上の整数の組![]() の個数です.
の個数です.
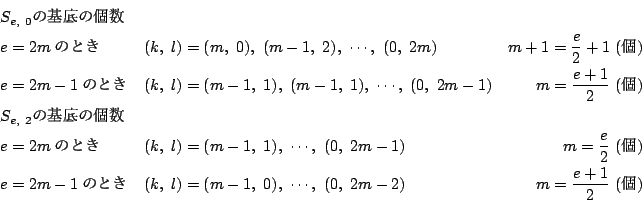
次に,![]() を調べます.
を調べます.
![]() のとき.
のとき.
![]() の要素
の要素![]() を
を
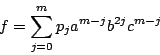
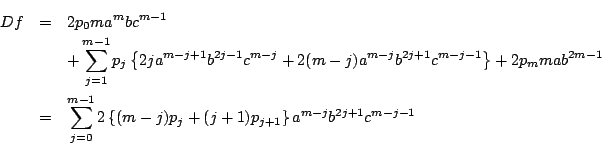
![]() のとき.
のとき.
![]() の要素
の要素![]() を
を
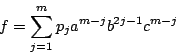
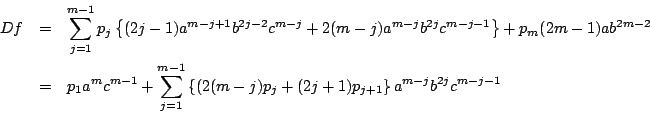
したがって,
いずれの場合も![]() は
は![]() から
から![]() 上への準同型写像となる.
その核の次元は
上への準同型写像となる.
その核の次元は![]() の次元から
の次元から![]() の次元を引いた差なので,
の次元を引いた差なので,
![]() 次の場合の基底は
次の場合の基底は
南海 とりあえずひとつの結論を得ることができた.