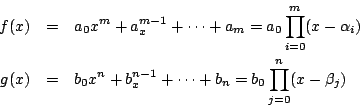
である.このとき
とおく.積
![]() を方程式
を方程式
![]() ,
または整式
,
または整式![]() の終結式という.
の終結式という.
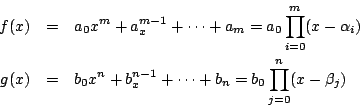
![]() を方程式
を方程式
![]() ,
または整式
,
または整式![]() の終結式という.
の終結式という.
定義からただちに
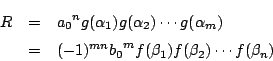
整式を明示したいときは![]() とも書こう.
とも書こう.
![]() は
は
![]() に関して対称で,
に関して対称で,
![]() に関して
に関して![]() 次である.
また
次である.
また
![]() に関して対称で,
に関して対称で,
![]() に関して
に関して![]() 次である.
これから
次である.
これから![]() は係数
は係数
![]() および
および
![]() の整式となる.
の整式となる.
耕介
![]() と
と![]() に共通根が存在することと
に共通根が存在することと
![]() が同値にになる,ということでしょうか.
が同値にになる,ということでしょうか.
南海
その通りである.
また終結式は![]() と
と![]() から
から![]() を消去し,
係数だけの関係を作ったのであるともいえる.
を消去し,
係数だけの関係を作ったのであるともいえる.
耕介
共通根があるということは,同じ![]() の値で成立することなので,
消去した関係が成り立つことと同値である,のですね.
の値で成立することなので,
消去した関係が成り立つことと同値である,のですね.
南海
その通りである.
そこで,![]() も
も![]() も2次式の場合,終結式を求めてみてほしい.
も2次式の場合,終結式を求めてみてほしい.
耕介
南海
この式はどこかで見たことがないだろうか.
文字が違うので気づかなかったかも知れない.
『数学対話』−「ポンスレの定理」の「楕円と円,![]() の場合」にある.このときは,消去法として用いた.
の場合」にある.このときは,消去法として用いた.