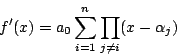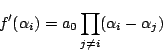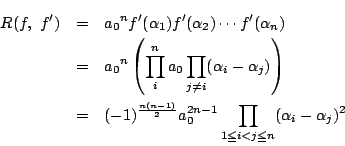この二つの同値性から考えて
南海
これはいいことに気づいた.
![]() と
と![]() が同値であることはその通りであるが,
それで一致するわけではない.
が同値であることはその通りであるが,
それで一致するわけではない.
![]() のとき,
のとき,![]() だった.
だった.
![]() を求めてみてほしい.
を求めてみてほしい.
耕介
![]() の根を
の根を![]() と
と![]() とします.
とします.
![]() ですから,この根は
ですから,この根は
![]() です.
です.
ですから根と係数の関係より
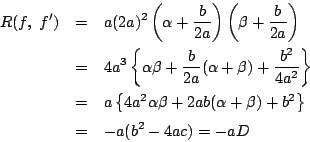
耕介 3次以上になるとこの方法では大変です. 一般的にはどのようにすればいいのですか.
南海
根の方から考えればよい.
記号はこれまでと同様とすると,
実は![]() の場合と同様に次の定理が成り立つ.
の場合と同様に次の定理が成り立つ.
証明