


次: 4次方程式
上: 3次方程式
前: 虚数の意義
南海
このように三次方程式が解けるようになったのは16世紀,
イタリアのカルダノ(Girolamo Cardano 1501.9.24 - 1576.9.21)からである.
カルダノの方法はもう少し技巧的だ.
それを背景にした入試問題が2000年信州大学で出されている.
「カルダノの方法」を話そう.カルダノは
と分解して, 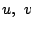 「二次方程式と3乗根」だけで求められるようにできないか,
ということだった.
「二次方程式と3乗根」だけで求められるようにできないか,
ということだった.
耕一 この 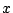 を代入するのですね.
を代入するのですね.
だからもし
となる 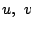 がとれればよい.
がとれればよい.
…あっ.これは解の公式のなかで, 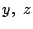 で作った式と同じです.
で作った式と同じです.
南海 だから当然同じ結果が得られるのだよ.
ここで,三次方程式の解法をまとめておこう.
の解公式を作る.
[第1段階]
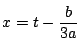 とおく.
とおく.
ここで
とおく.方程式1は
となる.
[第2段階]
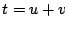 とおき2に代入する.
とおき2に代入する.
ゆえに
となるように 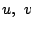 を定めれば,そのときの
を定めれば,そのときの 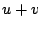 は2をみたし,解が得られる.
は2をみたし,解が得られる.
[第3段階]
3を満たす 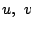 を求める.
を求める.
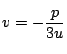 より
より
これから
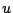 と
と 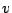 は対称なので符号は一方のみをとればよい.
は対称なので符号は一方のみをとればよい.
ここで 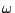 を1の3乗根,つまり
を1の3乗根,つまり
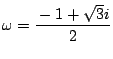 とする.
とする.
[第4段階]
ゆえに2の解は
の三つである.
ここで
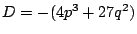 とおくと
とおくと
ともかく,重解を持つ場合以外はこれが三つの解であり, 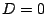 のときこれらのなかに同じものが
出来ることがわかる.
のときこれらのなかに同じものが
出来ることがわかる.
[第5段階]
1の解は
を代入し,
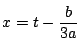 としたものである.
としたものである.
とおくと,



次: 4次方程式
上: 3次方程式
前: 虚数の意義
Aozora Gakuen
![]() を代入するのですね.
を代入するのですね.
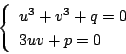
![]() で作った式と同じです.
で作った式と同じです.
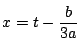 とおく.
とおく.
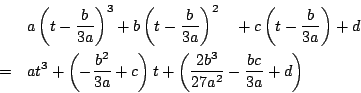
![]() とおき2に代入する.
とおき2に代入する.
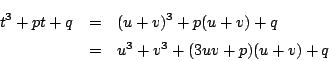
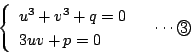
![]() を求める.
を求める.
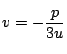 より
より
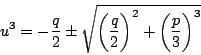
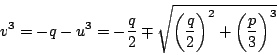
![]() と
と ![]() は対称なので符号は一方のみをとればよい.
は対称なので符号は一方のみをとればよい.
![]() を1の3乗根,つまり
を1の3乗根,つまり
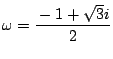 とする.
とする.
![\begin{eqnarray*}
∴ \quad u&=&\omega^k\sqrt[3]{-\dfrac{q}{2}
+\sqrt{ \left(\d...
...{q}{2} \right)^2+\left(\dfrac{p}{3}\right)^3}},\ \ (k=0,\ 1,\ 2)
\end{eqnarray*}](images/img135.gif)
![\begin{displaymath}
t=\left\{
\begin{array}{l}
\sqrt[3]{-\dfrac{q}{2}+\sqrt{ \l...
... \right)^2
+\left(\dfrac{p}{3}\right)^3}}
\end{array}\right.
\end{displaymath}](images/img136.gif)
![]() とおくと
とおくと
![\begin{displaymath}
t=\omega^k\sqrt[3]{-\dfrac{q}{2}+\dfrac{1}{6}\sqrt{-\dfrac{D...
...rac{q}{2}-\dfrac{1}{6}\sqrt{-\dfrac{D}{3}}},
\ \ (k=0,\ 1,\ 2)
\end{displaymath}](images/img138.gif)
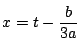 としたものである.
としたものである.
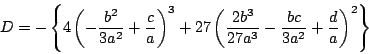
![\begin{eqnarray*}
x&=&-\dfrac{b}{3a}+\omega^k\sqrt[3]{-\dfrac{b^3}{27a^3}+\dfra...
...dfrac{d}{2a}-\dfrac{1}{6}\sqrt{-\dfrac{D}{3}}},\ \ (k=0,\ 1,\ 2)
\end{eqnarray*}](images/img140.gif)