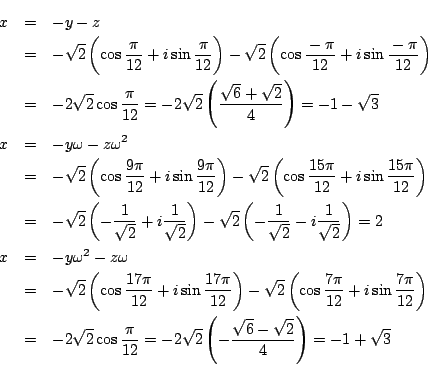次: カルダノの解法によるまとめ
上: 3次方程式
前: 三次方程式の判別式
南海 ところがここで不思議なことが起こった.
たとえば次の三次方程式を解いてみよう.
これは,暗算すると 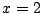 が見つかり因数定理から
が見つかり因数定理から
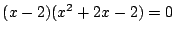 となって解ける.
つまり三つの実数解
となって解ける.
つまり三つの実数解
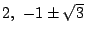 をもつ.
をもつ.
これが上の一般的な方法ではどのようになるかやってみてほしい.
耕一 やってみます.
より
これから
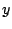 として
として
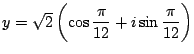 を
使います.すると,
を
使います.すると,
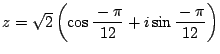 です.したがって
です.したがって
南海
すると一般的にやろうとすると,最後は三つの実数解が得られるのにもかかわらず,
途中の計算では虚数が登場する.実数解になる場合は,
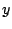 と
と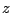 が共役な複素数になるわけだ.
だからもし虚数を認めないと,この一般論で実数の解が得られないことになる.
イタリアでは虚数を用いることについての論争があったのだが,このようにして,
虚数の存在が人々に認識されるようになっていったのだ.
が共役な複素数になるわけだ.
だからもし虚数を認めないと,この一般論で実数の解が得られないことになる.
イタリアでは虚数を用いることについての論争があったのだが,このようにして,
虚数の存在が人々に認識されるようになっていったのだ.
Aozora Gakuen
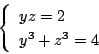
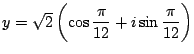 を
使います.すると,
を
使います.すると,
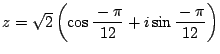 です.したがって
です.したがって