次： 代数的整数 上： 原始多項式 前： 原始多項式

因数分解のアルゴリズム

耕一　 必ず因数分解できる方法というのはあるのでしょうか．

南海　 「必ずできる方法」を何というのか．

耕一　 「アルゴリズム」です．

南海　 つまり「因数分解のアルゴリズム」はあるのか？　ということだ．

因数分解についてどんな方法を知っているか．

耕一　$x$の整式を因数分解する方法は次のものしか知りません．

1. 二次式$ax^2+bx+c$は，二次方程式$ax^2+bx+c=0$ の 二つの根 $\alpha,\ \beta$をもちいて次のように因数分解される．
   
   $$ax^2+bx+c=a(x-\alpha)(x-\beta)$$
   
   

2. 因数定理で一次の因数を発見し，次数を下げる．
3. 適当な置き換えによって二次式として分解し，それを繰り返す．

しかし，因数定理で因数を発見するというのは，方程式の根を暗算で見つけるということですから いつもそれでできるとはかぎりません．

因数を発見する一般的な方法はあるのでしょうか． したがってまた，因数がない，つまり既約であることを証明する方法は あるのでしょうか．

南海　 たいへん難しい問題だが， 整数係数の多項式のの整数係数の因数を発見するアルゴリズムは，これがあるのである！　

$f(x)$を$x$の整数係数の$n$次の整式としよう．

1. $f(x)$の因数は，$\dfrac{n}{2}$ 以下のものでさがせばよい． $\dfrac{n}{2}$ を超えない最大の整数を $s$ とする．
2. $g(x)$ を $f(x)$ の因数とすれば $g(x)$ は $f(x)$ を割り切る．
3. $s+1$ 個の相異なる整数 $a_0,a_1, \cdots a_s$ を選ぶ．
4. $f(a_0),f(a_1),f(a_2), \cdots f(a_s)$ は $g(a_0),g(a_1),g(a_2), \cdots g(a_s)$ で割り切れる．
5. $f(a_0),f(a_1),f(a_2), \cdots f(a_s)$ をそれぞれ因数分解し，約数を選ぶ． 選び方の組み合わせ方は有限個である．
6. これらの値を $g(a_0),g(a_1),g(a_2), \cdots g(a_s)$ の値とする $g(x)$ をラグランジュの補間公式で構成する．
7. このとき， $g(x)$ の係数が整数であることなどを用いて， 可能なものを限定するとよい．
8. すべての $f(x)$ の整数係数の因数は， 約数の組み合わせ方をかえててできる有限個の $g(x)$ の中にしかない． 実際に割ってさがす．ひとつもなければ，既約である．

「ラグランジュの補間公式」は『新作/改作問題』「ラグランジュの補間公式」を見てほしい．

この方法で， $f(x)=x^4+x^2+1$ を因数分解しよう．

耕一　 でも $x^4+x^2+1=(x^2+1)^2-x^2=(x^2+x+1)(x^2-x+1)$ですね．

南海　 これがこの方法ではどうなるかやってみるのだ．

1. 4次の$x$の整数係数の整式 $f(x)$ の因数で2次以下のものを求める．

   $g(x)$ を2次以下の$f(x)$ の因数とすれば $g(x)$ は $f(x)$ を割り切る．

2. 3個の相異なる整数として，$0,\ 1,\ -1$ を選ぶ． $f(0)=1,\ f(1)=3,\ f(-1)=3$ である． $f(0)=1,\ f(1)=3,\ f(-1)=3$ の因数を， $A,\ B,\ C$ とする．
3. 
   
   $$g(x)=A\dfrac{(x-1)(x+1)}{(0-1)(0+1)}+B\dfrac{(x-0)(x+1)}{(1-0)(1+1)}+ C\dfrac{(x-0)(x-1)}{(-1-0)(-1-1)}$$
   
   
   とおく．つまり
   
   $$g(x)=-A(x-1)(x+1)+\dfrac{B}{2}(x-0)(x+1)+\dfrac{C}{2}(x-0)(x-1)$$
   
   

4. $A,\ B,\ C$のうち一つの符号は任意にとれるので$A=1$ とする．
   
   $$g(x)=\left(-1+\dfrac{B+C}{2}\right)x^2+\dfrac{B-C}{2}x+1$$
   
   

5. $B,C= \pm 1, \pm 3$ の16通りの組み合わせがある．

   ガウスの定理4により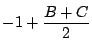， $-1+\dfrac{B+C}{2}$が$\pm 1$ のものだけを考えればよい．よって
   

   $$(B,C)= (1,\ 1),\ (3,\ -1),\ (-1,\ 3),\ (3,\ 1),\ (1,\ 3),\ (1,\ -1),\ (-1,\ 1),\ (3,\ -3),\ (-3,\ 3)$$
   
   

6. 各々 $g(x)$ を求めると， $1,2x+1,\ -2x+1$, $\underline{x^2+x+1},\ \underline{x^2-x+1}$, $-x^2+x+1,\ -x^2-x+1,\ -x^2+3x+1,\ -x^2-3x+1$．
7. 下線を引いた2つが， $f(x)$ を割り切る．よって $f(x)=(x^2+x+1)(x^2-x+1)$

南海　 大切なことは，「必要条件で絞る方法がある」ということだ． 必要条件は個別に工夫すればよいが，最後の手があるのだ．