証明
![]() ,
,![]() を
を![]() 次,
次,![]() 次の原始多項式とする.
次の原始多項式とする.
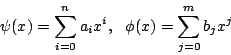
任意の素数![]() をとる.
をとる.![]() で割り切れない係数をもつ最低次の項を
で割り切れない係数をもつ最低次の項を
![]() とする.
とする.
積
![]() における
における![]() 次の項の係数は
次の項の係数は
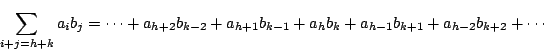
ここで中央の![]() は
は![]() で割れないが,
他のすべての
で割れないが,
他のすべての![]() は
は![]() の倍数になる.つまりこの係数は
の倍数になる.つまりこの係数は![]() で割り切れない.
で割り切れない.
任意の素数![]() について,
について,![]() で割りきれない係数の項が存在するので,
積
で割りきれない係数の項が存在するので,
積
![]() の係数の最大公約数は1である.つまり積は原始多項式である.□
の係数の最大公約数は1である.つまり積は原始多項式である.□
次の定理の証明のために一つ補題を示そう.
この補題は,整数
![]() の最大公約数が1なら,
の最大公約数が1なら,
この証明は『初等整数論』「一次不定方程式」「一次不定方程式の解の存在」定理5を見てほしい.
証明
二式
![]() は同次なので
は同次なので
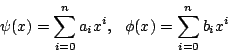
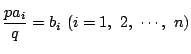 で
で
![]() は互いに素なので
は互いに素なので
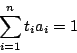
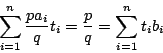
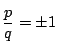 である.□
である.□
南海 そこで本題.
証明
![]() の係数の最大公約数を
の係数の最大公約数を![]() とする.
とする.![]() は整数である.
は整数である.
![]() とおく.
とおく.![]() は原始多項式である.
は原始多項式である.
![]() に係数の分母の最小公倍数をかけ,それから係数の最大公約数でくくると原始多項式が得られる.それを
に係数の分母の最小公倍数をかけ,それから係数の最大公約数でくくると原始多項式が得られる.それを![]() とし,
とし,
![]() とおく.
とおく.![]() は有理数である.
は有理数である.
同様に
![]() (
(![]() は有理数,
は有理数,![]() は原始多項式)とする.
は原始多項式)とする.
ガウスの定理(4)より
![]() は原始多項式なので,補題1より
は原始多項式なので,補題1より
![]() となり
となり![]() は整数である.ゆえに
は整数である.ゆえに![]() は2つの整数係数の多項式
は2つの整数係数の多項式
![]() ,
,![]() に因数分解された.□
に因数分解された.□
南海 ここまで来ると,例題の(2)を一般化することができる.
証明
この多項式を![]() とする.
とする.![]() が因数分解されたとする.それを
が因数分解されたとする.それを
![]() とし,
その次数を
とし,
その次数を![]() とする.
とする.
ガウスの定理の証明と同様に素数![]() に対し,
に対し,
![]() の
の
![]() で割り切れない係数をもつ最低次の項を
で割り切れない係数をもつ最低次の項を
![]() とする.
とする.
積
![]() における
における![]() 次の項の係数は
次の項の係数は
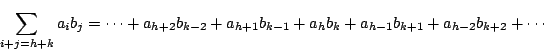
ゆえに![]() の定数項は
の定数項は![]() で割り切れ,条件と矛盾し,対偶が示せた.□
で割り切れ,条件と矛盾し,対偶が示せた.□
南海 以上の一般論が例題の別解になっていることがわかっただろうか.
耕一
もういちどまとめます.
![]() が有理数
が有理数![]() を用いて
を用いて
![]() と因数分解されるとき,
と因数分解されるとき,
![]() を
を
![]() とすれば
とすれば
![]() と因数分解される.この
と因数分解される.この![]() が直ちに整数係数とはいえないが,さきにいわれましたように,今の場合
が直ちに整数係数とはいえないが,さきにいわれましたように,今の場合![]() の係数は互いに素
なので,ここからくくって
の係数は互いに素
なので,ここからくくって![]() 全体にかける整数はないので,
全体にかける整数はないので,![]() 自身が整数係数である.
すると同じ記号を用いて
自身が整数係数である.
すると同じ記号を用いて![]() より
より![]() となり
となり![]() は整数である.
は整数である.
例題の最後の問題は,対偶を示すことは同じで,
有理数解があれば整数解で![]() が整数の因数をもつが,アイゼンシュタインの既約性定理から
が整数の因数をもつが,アイゼンシュタインの既約性定理から
![]() は既約なので,それはあり得ない.
は既約なので,それはあり得ない.
南海
ということだ.
![]() のところは,次のようにしても良い.
のところは,次のようにしても良い.![]() の係数の
分母の最小公倍数と,分子の最小公倍数を括りだし,
の係数の
分母の最小公倍数と,分子の最小公倍数を括りだし,
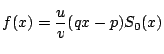 と表したとする.
ここで
と表したとする.
ここで![]() は原始多項式である.
は原始多項式である.![]() も原始多項式で,
も原始多項式で,![]() も原始多項式なので,ガウスの定理と
補題から
も原始多項式なので,ガウスの定理と
補題から
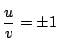 .これでも良い.
.これでも良い.