![]() を実数とし,三次方程式
を実数とし,三次方程式 ![]() の三つの解を
の三つの解を
![]() とする.
このとき
とする.
このとき
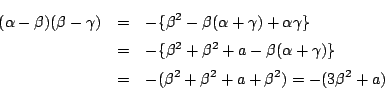
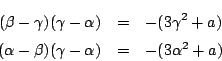
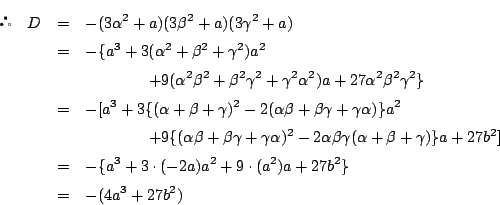
耕一 この式の形は見たことがあります.
南海 次の形では入試問題などにもよく出される. つまり,相異なる三つの実数解をもつための必要十分条件を関数のグラフからも導く. 求めてみてほしい.
耕一
![]() とおきます.
とおきます.![]() なので,
なので,![]() が必要で,このとき
が必要で,このとき
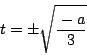
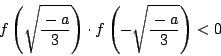
南海
![]() が相異なる実数をもち
が相異なる実数をもち![]() が極値をもつときは
二つの方法を比較することで,判別式
が極値をもつときは
二つの方法を比較することで,判別式![]() の意味がよくわかる.
の意味がよくわかる.
積
![]() が負のときは
が負のときは ![]() で,
極大値と極小値が異符号であり,もとの三次方程式
で,
極大値と極小値が異符号であり,もとの三次方程式 ![]() は3実数解をもつ.
この積が0なら,
は3実数解をもつ.
この積が0なら,![]() であり,
であり,![]() は
は ![]() 軸に接するので,
軸に接するので,![]() は重解をもつ.
積
は重解をもつ.
積
![]() が正のときは
が正のときは ![]() で実数根は一つしかない.
で実数根は一つしかない.
ついでに,二次方程式
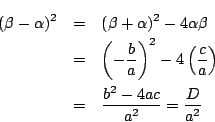
耕一 判別式とは,異なる根の差の平方の積
に,最高次数の係数の平方がかかったものなのでね.
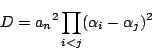
平方しているのでどの二つを入れ替えても変わらず,根
![]() の対称式なので,
根と係数の関係からもとの方程式の係数で書けるのですね.
の対称式なので,
根と係数の関係からもとの方程式の係数で書けるのですね.