拓生 どんな問題ですか.
秀樹
いちばんはっきりしている例でいうと, ![]() が実数全体を動くとき,
が実数全体を動くとき,
点![]() を満たすことはいろんなやり方でわかりますが,
を満たすことはいろんなやり方でわかりますが,![]() だけにはなれず,
円からこの点を除外しなければならないのです.
だけにはなれず,
円からこの点を除外しなければならないのです.
![]() 座標は
座標は
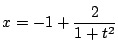 と変形できるから,確かに
と変形できるから,確かに![]() にはなり得ないのだけれ
ど何かわざとらしい変形で,よく見落とします.
にはなり得ないのだけれ
ど何かわざとらしい変形で,よく見落とします.
南海 除外点とはどんな点なんだろう.
秀樹 どんな点といわれても除外されて無い点なんですが.
拓生
でも![]() って次のように
って次のように![]() のときの極限です.
のときの極限です.
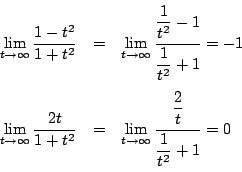
秀樹 無限の点なんてあるのかなあ.
南海 たとえば中学生に「二乗して負になる数は」と聞いたら「あるはずない」 というだろうけれど,複素数を習えばちゃんとあるわけだから,この場合も何かある可能性がある.
拓生
複素数のときは![]() とはじめは無理に作ったようですが,
実際は複素数の方が自然で広い世界だった….
とはじめは無理に作ったようですが,
実際は複素数の方が自然で広い世界だった….
この場合も無限遠点を作ってしまえばいい. ![]() が実数 全体と無限遠点を動くとき,
軌跡は円全体になる….
が実数 全体と無限遠点を動くとき,
軌跡は円全体になる….
秀樹 作るといってもそんな勝手にできるのだろうか.
南海 少なくとも数学的に式でとらえることができて,これまでの実数 と一体になったものでなければならない. 結局は,計算できるものとしてとらえることができたとき,現実にそれは存在するといえる.
拓生 どうするのでしょうか.
南海 それのヒントになることは,実はすでに君たちはよく知っているのだよ. あるやり方では「無限」の場合がとらえられないが,あるやり方では「無限」の場合を含めて 統一的にやれることがあっただろう.
秀樹
直線を![]() と表せば,
と表せば, ![]() 軸に平行な
軸に平行な![]() の型の直線は傾きが無限
のときになり,別に扱わなければならないが,直線を
の型の直線は傾きが無限
のときになり,別に扱わなければならないが,直線を![]() と表せば,
と表せば, ![]() 軸に平行な
場合を含めて一つの式で表せる.
軸に平行な
場合を含めて一つの式で表せる.
拓生
直線を![]() と三つの数の組
と三つの数の組
![]() で表すと,
で表すと,
南海 そう.
拓生
無限遠点をとらえるためには,![]() でない
数の組
でない
数の組![]() を考える.
を考える.
![]() なら
なら![]() と
と![]() は
同じ点を表すとする.すると,
は
同じ点を表すとする.すると,![]() なら
なら![]() と
と
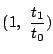 は同
じ点だから,
は同
じ点だから,![]() である全体は
である全体は
![]() と対応させれば実数全体と一致
する.
と対応させれば実数全体と一致
する.![]() の点は結局
の点は結局![]() で定まる1点で,これが無限遠点です.
で定まる1点で,これが無限遠点です.
秀樹
軌跡の式とうまくあうかな.
![]() を代入して
分母を整理すると,
を代入して
分母を整理すると,
南海 このやり方で実数全体と無限遠点をあわせたものを「射影直線」といいます.
秀樹
媒介変数![]() が射影直線の全体を動くとき,
軌跡が円全体になるのか.この方がずっとすっきりする.
が射影直線の全体を動くとき,
軌跡が円全体になるのか.この方がずっとすっきりする.
拓生
でも直線上の点が二つの数の組![]() で表されるのなら,
平面上の点
で表されるのなら,
平面上の点 ![]() も三つの数の組
も三つの数の組
そうかこれが「射影平面」ですね,つまり![]() でない数の組
でない数の組
![]() を考える.
を考える.
![]() なら
なら
![]() と
と
![]() は
同じ点を表すとする.すると,
は
同じ点を表すとする.すると,![]() なら
なら
![]() と
と
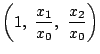 は同じ点だから,
は同じ点だから,![]() で
ある全体は普通の平面になる.
で
ある全体は普通の平面になる.![]() のときは
のときは
![]() になる …,これは何だ,
あっ,そうか射影直線になる.
になる …,これは何だ,
あっ,そうか射影直線になる.
この場合は無限遠直線ということですね.
秀樹
どのみち
![]() だから同じことだと思うけど.
だから同じことだと思うけど.
拓生 この場合はね.
秀樹 平行な二直線は無限遠点で交わるということになるのでしょうか.
拓生
やってみましょう.平行な二直線を
射影平面の座標を
![]() とする.
とする.![]() のときは
のときは
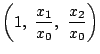 でこれが今までの平面になる.だから,
直線の式を射影平面の式にするために,
でこれが今までの平面になる.だから,
直線の式を射影平面の式にするために,
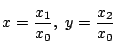 を代入し
て分母を払うと,
を代入し
て分母を払うと,
南海 話はつきないようであったが,射影平面が定義されたので, とりあえずもう一つの話をしなければならない.