 例 1.6.1
例 1.6.1
拓生 どういうこと.
秀樹 図と問題を見て下さい.
 例 1.6.1
例 1.6.1
証明
円の方程式を![]() として一般性を失わない.
として一般性を失わない.
![]() と
と ![]() の座標を
の座標を
![]() とする.
とする.
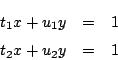
これらが ![]() を通るので,
を通るので,
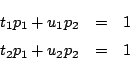
![]() が直線
が直線![]() の上にあるので,
の上にあるので,
![]() である.
ところがこの式は
である.
ところがこの式は ![]() が
が![]() の上にあることを示している.□
の上にあることを示している.□
秀樹 (1)でも(2)でも係数と変数の位置が入れ替わっています. たまたまうまくいっただけではないのか,と思うのです.
拓生 だ円や双曲線,放物線の接線の式は?
秀樹
だ円,双曲線,放物線
拓生
これらの式は,
![]() に関して対称です.
に関して対称です.
秀樹 そうか,たまたまではなく,二次曲線の性質なのか.
拓生
二次曲線は一般には
秀樹 数IIIの微分で習ったことを用いて計算する.
まず
![]() の両辺を
の両辺を ![]() で微分すると
で微分すると
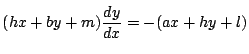 .したがって,点
.したがって,点
ここで,
![]() を用いて整理すると,
を用いて整理すると,
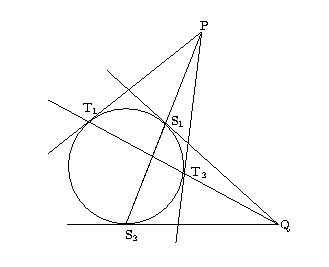
すると,先の円についての演習問題【 ![]() から二本の接線を引く.接点を
から二本の接線を引く.接点を![]() とする.
直線
とする.
直線![]() 上の任意の点
上の任意の点 ![]() をとる.
をとる. ![]() から二本の接線を引く.接点を
から二本の接線を引く.接点を
![]() とする.すると
とする.すると ![]() は再び直線
は再び直線![]() の上にある 】 は任意の二次曲線
で成り立つのか!
の上にある 】 は任意の二次曲線
で成り立つのか!
拓生 でも二次曲線を一般的に考えると,二本の接線が平行になることもある. そのときも射影平面で考えると無限遠点で交点はある!