もちろん,普通の平面の場合と同様,これが因数分解されて二つの直線などになる場合もある. どのようなときにだ円になったりするのかという二次曲線の分類は 『数学対話』「三角形に辺の中点で内接する楕円(シュタイナー楕円)」を 参考にしてもらいたい.
さて,この式が何かの二次曲線を表しているとする.
このとき,曲線上の点
![]() に対して
に対して

拓生
いちいち
![]() で書くのは大変ですね.
で書くのは大変ですね.
南海
そう.大変だ.何とか簡単にしたいというのは
大切なことだ.そこで,
![]() とし,
とし, ![]() の式を
の式を![]() と書こう.
また接線の式を
と書こう.
また接線の式を![]() とおこう.
とおこう.
拓生
ずいぶん簡単ですね.すると接線の対称性は
秀樹 先の問題の証明は次のようになるのですね.
これが一般の二次曲線についての証明です.
南海
点 ![]() のことを極,
直線
のことを極,
直線![]() のことを極線といいます.
のことを極線といいます.
秀樹 でもこれだけだと何かたいそうなだけですね.ここから導かれる性質 があれば教えて下さい.
南海 パスカルの定理を証明してみよう.
拓生 パスカルの定理って聞いたことがあります.
 円上の6点を定め番号を打つ.各点から,一つ手前とひとつ後の番号の点を結ぶ.
円上の6点を定め番号を打つ.各点から,一つ手前とひとつ後の番号の点を結ぶ.
南海 そう,これがパスカルの定理だ.点の番号の付け方は任意だ. この図は3交点が円の中に来る場合だ.
この証明は,パスカルが16歳のときに発見したもので大変美しい定理だ.そしてその後の 射影幾何学の始まりとなるものだ.ぜひ証明を考えてほしい.
これは一般の二次曲線で成立する.
その準備として,次の補題を確認する.
二次曲線 ![]() 上の点
上の点 ![]() での接線
での接線 ![]() を
を
![]() とおく.
とおく.
1.

である.
2.式の形より
が成り立つ.
3.さらに,どの三つも同一直線上に無い5点が与えられれば, この5点を通る二次曲線がただ一つ定まる.
(1)(2)は済んでいる.(3)は
![]() と係数が5個あり,
同一直線上にない5点が
と係数が5個あり,
同一直線上にない5点が ![]() を満たせば係数の比が確定することからわかる.
厳密な論述は連立一次方程式と行列論が必要である.
を満たせば係数の比が確定することからわかる.
厳密な論述は連立一次方程式と行列論が必要である.
証明
同様に二次曲線
二つの二次曲線の式は定数倍を除いて一致する.
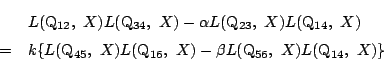
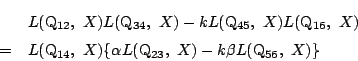
左辺に
![]() を代入すると0になるので,右辺も満たす.
そして
を代入すると0になるので,右辺も満たす.
そして
![]() は
は
![]() 上にはない.よって,
上にはない.よって,
ここで,
![]() と置くとこの式は
と置くとこの式は
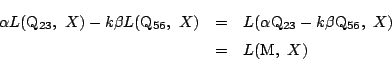
つまり,直線
![]() は直線
は直線
![]() と一致する.
と一致する.
同様に,直線
![]() は直線
は直線
![]() と一致し,
直線
と一致し,
直線
![]() は直線
は直線
![]() と一致する.
と一致する.
(1)より