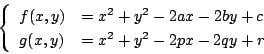
二つの二次式
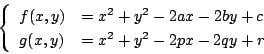
根軸とは二つの円が交わっているときは,二つの共有点を通る直線だが, この直線は,二つの円への接線の長さが等しい点の軌跡でもある. この観点からすると,二円が交わらなくても意味をもつ.
ここで「二つの円への接線の長さが等しい」としたところを, 「二つの円への接線の長さの比が等しい」と変えるとどうなるか.
拓生
記号は上と同じにします.点
![]() から二円への接線の長さは,
先の定理の証明と同様に
から二円への接線の長さは,
先の定理の証明と同様に

あっ.これはまた根軸が同じになる円になる.
南海 そうなのだ.二つの円
![]() に対して
に対して
![]() のときの意味などを考えればおもしろいはずだが,今は次のことを確認しておこう.
のときの意味などを考えればおもしろいはずだが,今は次のことを確認しておこう.
これを用いると次の事実が示される.
補題 4
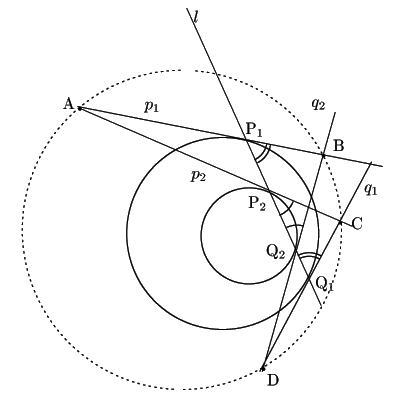 一つの直線
一つの直線 ![]() が,
二つの円
が,
二つの円 ![]() に,
それぞれ
に,
それぞれ
![]() と
と
![]() で交わっている.
これらの交点におけるそれぞれの円の接線を
で交わっている.
これらの交点におけるそれぞれの円の接線を
![]() とする.
このとき
とする.
このとき ![]() と
と![]() ,
,![]() と
と![]() ,
,![]() と
と![]() ,
,![]() と
と![]() の交点
の交点
![]() ,
,![]() ,
,![]() ,
,![]() は,
二つの円
は,
二つの円 ![]() と根軸を共有する同一円の周上にある.
と根軸を共有する同一円の周上にある.
証明
![]() と
と ![]() の交点での接線が
の交点での接線が ![]() となす角を
となす角を
![]() とする.
また図のように接線と円との交点を
とする.
また図のように接線と円との交点を
![]() とする.
とする.
![]() ,
,
![]() ,
,
![]() ,
,
![]() に正弦定理を用いると,
に正弦定理を用いると,
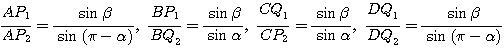
したがって![]() ,
,![]() ,
,![]() ,
,![]() は二円への接線の長さの比が
等しいので,この二円と根軸を共有するある円の周上にある.□
は二円への接線の長さの比が
等しいので,この二円と根軸を共有するある円の周上にある.□