次： 複素射影空間内での証明 上： 二次曲線の閉形定理 前： 二次曲線の閉形定理

二曲線の位置関係，複素数の導入

南海　 われわれは入試問題から出発したので，二つの二次曲線は相互に離れている場合しか考えなかった． 二つの二次曲線の位置関係はもちろんいろいろあり得る．

次のようなときにもポンスレの閉形定理を考えることができるのではないか．

拓生　 $C_1$上の 点$\mathrm{P}_1$から$C_0$に接線を引き， 接線上にある$C_1$の上のもう一つの点を$\mathrm{P}_2$とする．

点$\mathrm{P}_2$から$C_0$に接線を引き， 接線上にある$C_1$の上のもう一つの点を$\mathrm{P}_3$とする．

点$\mathrm{P}_3$から$C_0$に接線を引き， 接線上にある$C_1$の上のもう一つの点を$\mathrm{P}_4$とする．…．

これを繰りかえして，元の$\mathrm{P}_1$に戻ってくるかということですね．

ある点$\mathrm{P}_1$からはじめて$n$回で元に戻れば，どこからはじめても元に戻るか．

確かにこのように考えれば，位置関係は自由です．

南海　 しかし，このような場合，$C_0$と$C_1$の両方に接する接線が存在しうる．

拓生　 その場合，$C_1$の方の点を$\mathrm{P}_1$とすると

$$\mathrm{P}_2=\mathrm{P}_1,\ \mathrm{P}_3=\mathrm{P}_2,\ \cdots$$

となりませんか． つまり共通接線の接点は，$n$が2でも3でもいくらでも，条件を満たす点である．

南海　 共通接線は何本あるのだろう．

拓生　 4本，3本，2本，なし，のいろいろあります．

南海　 そこで先に考えた円と円で$n=3$の場合の例をもう一度考えよう．

$$C_0\ :\ x^2+y^2=1,\ C_1\ :\ (x-a)^2+y^2=r^2$$

であった．$C_1$上の点 $\mathrm{P}(x,\ y)$が媒介変数$t$を用いて

$$x-a=\dfrac{r(1-t^2)}{1+t^2},\ y=\dfrac{2rt}{1+t^2}$$

と表され，点$\mathrm{Q}$も同様に媒介変数$s$で表されるとき， 直線$\mathrm{PQ}$が$C_0$と接するための条件は

$$T(s,\,t)=\{(r-a)st+r+a\}^2-(st-1)^2-(s+t)^2$$

であった．そして$\mathrm{P}$からはじめて， 接線の他の交点を $\mathrm{Q},\ \mathrm{R},\ \mathrm{S}$ととるとき， $\mathrm{S}=\mathrm{P}$となるための必要十分条件が

$$\begin{eqnarray*} H(t)&=&<(r-a)\{(r+a)^2-t^2-1\}+(r+a)[\{(r-a)^2-1\}t^2-1]>^2\\ &&\quad \quad -\{(r+a)^2+(r-a)^2t^2\}^2 \end{eqnarray*}$$

とおくとき，$H(t)=0$となるのであった．

そこで，共通接線との関連を調べよう．

$C_1$上の点 $\mathrm{P}(x_1,\ y_1)$が

$$x_1-a=\dfrac{r(1-t^2)}{1+t^2},\ y_1=\dfrac{2rt}{1+t^2}$$

と表されるとき， 点$\mathrm{P}$での接線が$C_0$とも接するための$t$に関する条件を求めてみてほしい．

拓生　 接線の式は

$$(x_1-a)(x-a)+y_1y=r^2$$

これが$C_0$とも接すればよいので

$$\dfrac{-a(x_1-a)-r^2}{\sqrt{(x_1-a)^2+{y_1}^2}}=1$$

ここで $(x_1-a)^2+{y_1}^2=r^2$なので，条件は

$$\{a(x_1-a)+r^2\}^2-r^2=0$$

この式を因数分解して $x_1-a=\dfrac{r(1-t^2)}{1+t^2}$を代入する．

$r$を約して整理する．

$$\{(r-a-1)t^2+r+a-1\}\{(r-a+1)t^2+r+a+1\}=0$$

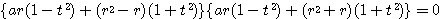
これは定数倍を除くと$H(t)$と同じ式だ．

$H(t)=0$は共通接線を与える式なのか．でもそれが虚根ということは?

南海　

$$x^2+y^2=1,\ (x-a)^2+y^2=r^2$$

の共通接線を実際に求めてほしい．

拓生　 共通接線を$mx+ny+1=0$とおきます．両方と接するので

$$\dfrac{1}{\sqrt{m^2+n^2}}=1,\ \dfrac{\vert ma+1\vert}{\sqrt{m^2+n^2}}=r$$

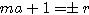です．これから ．また．

だから接線は

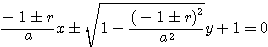　(第一，第三複号同順)

となりますが，根号内が負になるときはもう$xy$平面での直線ではありえません．

南海　 しかし，それぞれの円の式と連立させて共通根を求めれば，それが重根になることはまちがいない． もちろん点と直線の距離の式は使えないが，$x$か$y$を消去して得られる二次式の判別式をとれば， 距離の式から得られる式と同じ式が得られる．つまり虚根も考えれば， 上の接線の式は$C_0,\ C_1$の双方と重根をもつ． そういう意味ではもとの二つの二次曲線とそれぞれ重根をもつ共通接線が4本ある，ということにならないか．

そしてその共通接線を与える方程式が$H(t)=0$と一致した．

拓生　 それで思い出したのですが，円と二次曲線のいくつかの実例では， すべて最後に点$\mathrm{P}$を媒介変数表示したときの変数$t$についての四次方程式が得られました． そしてそれが恒等的に0になることを示そうとしました．

恒等的に0になるためには，実根でなくても虚根を含めて， しかも重根の場合は重複度も含めて，次数より1多い根があればそれで恒等的に0になるのでした． 図形から出発したので実数解ばかり考えますが，恒等式かどうかの判断は実数でなくてもよい．

南海　 そうだ．あわせて考えをまとめると

1. 共通接線の$C_1$側の接点$\mathrm{P}$は， 順次$\mathrm{P}_2$から作っていっても同じ$\mathrm{P}$になる． つまり$n$がいくらであっても元に戻る点である．
2. だからその点を媒介変数表示する変数$t$の値は， 点$\mathrm{P}$が元に戻る点であるための必要十分条件を表す四次方程式 を満たすはずだ．
3. それがとりもなおさず共通接線を与える方程式になる．
4. 恒等的に0になるためには，実根でなくても虚根を含めて， 重根の場合は重複度も含めて，次数より1多い根があればよい．
5. 虚数係数のものを含めれば$C_0,\ C_1$と重根をもつ共通接線は四本ある． この四本に対応するのが，先に得られた四次方程式の四つの根である．
6. したがって共通接線以外に一つでも元に戻る点があれば任意の点からはじめて 元に戻る．

拓生　 これはポンスレの閉形定理の証明になっていますね．

南海　 念のため，その他の場合も$H(t)=0$の根と共通接線の関係を確認しておいてほしい．

拓生　

1. 放物線と円で$n=3$のとき．
   
   $$H(t)=(b-a-1)(b-a+1)\{a^2t^4+2a(b-2a)t^2+b^2-1\}$$
   $H(t)=0$を$t^2$の二次方程式と見て0以上の解をもつ条件と共通接線の個数の関係を調べればよい．

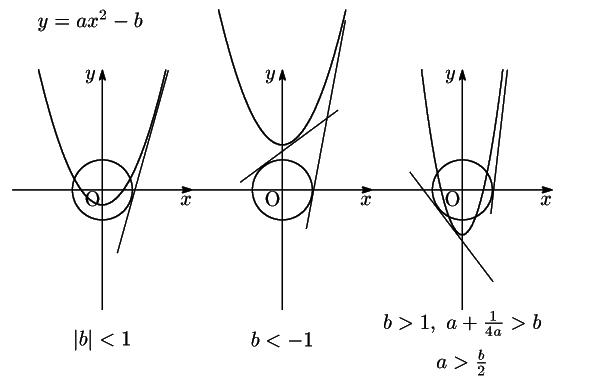
   $b^2-1\le 0$なら$t^2\ge 0$の解は一つ． $t^2>0$の解が二つになるのは，
   

   $$\left\{ \begin{array}{l} D>0\quad \iff\quad a+\dfrac{1}{4... ... -(b-2a)>0\quad \iff\quad a>\dfrac{b}{2} \end{array} \right.$$
   
   
   のとき． これは$b<-1$か $b>1,\ a+\dfrac{1}{4a}>b,\ a>\dfrac{b}{2}$のときで， 位置関係はそれぞれ図のようになり，共通接線はそれぞれ2本，4本，4本である．

2. 楕円と円で$n=3$のとき．
   $$\begin{eqnarray*} H(t)&=&(ab+a+b)(ab+a-b)(ab-a+b)(ab-a-b) \\ &&\quad \times \{b^2(1-a^2)t^4+2(2a^2-b^2-a^2b^2)t^2+b^2(1-a^2)\} \end{eqnarray*}$$
   
   
   なので2根の積は1．$H(t)=0$が実数解をもつのは$a$か$b$が1で接する場合を除くと
   
   $$D/4=4a^2(a^2-b^2)(1-b^2)> 0,\ 軸：-\dfrac{a^2-b^2+a^2(1-b^2)}{1-a^2}> 0$$
   
   
   のとき．これは$a<1<b$または$b<1<a$なので，確かに4つの共通接線をもつときである．

共通接線の交点の方程式は求めていませんが，$H(t)=0$が実根をもつ場合と 共通接線が存在する場合との同値性から，同じ式になることもまちがいありません．

南海　 式は求めればできるが，求めなくても一致することはまちがいない．それでいいでしょう．

次： 複素射影空間内での証明 上： 二次曲線の閉形定理 前： 二次曲線の閉形定理