拓生
媒介変数を射影直線にすることで,例えば楕円の場合に![]() を除くという例外がなくなる.
また,二次曲線を射影平面で考えることで,放物線と円の場合にあった,
「
を除くという例外がなくなる.
また,二次曲線を射影平面で考えることで,放物線と円の場合にあった,
「![]() 座標が
座標が![]() と異なる
と異なる![]() 上の点」という例外がいらなくなる.
上の点」という例外がいらなくなる.
南海 そうだ.そこで話を進めよう.
射影直線![]() を次のように定める.
を次のように定める.
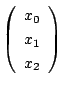
![]() でない複素数の組
でない複素数の組![]() の集合を考え,
の集合を考え,
![]() となる複素数
となる複素数![]() が存在するとき,
この二つの組は同じものとする.
複素数の組
が存在するとき,
この二つの組は同じものとする.
複素数の組![]() の集合で,
このようにして比が等しいものを射影直線といい,
の集合で,
このようにして比が等しいものを射影直線といい,![]() と表す.
一次元射影空間ともいう.
と表す.
一次元射影空間ともいう.
同様に
射影平面![]() を次のように定める.
を次のように定める.
![]() でない複素数の組
でない複素数の組
![]() の集合を考え,
の集合を考え,
![]() となる複素数
となる複素数![]() が存在するとき,
この二つの組は同じものとする.
複素数の組
が存在するとき,
この二つの組は同じものとする.
複素数の組
![]() の集合で,
このようにして比が等しいものを射影平面といい,
の集合で,
このようにして比が等しいものを射影平面といい,![]() と表す.
今後,
と表す.
今後,
![]() を必要に応じて
を必要に応じて![]() のような大文字で表そう.
のような大文字で表そう.
拓生
二次曲線 ![]() を射影座標で表す.「パスカルの定理」によれば,
を射影座標で表す.「パスカルの定理」によれば,
このとき![]() 上の点
上の点
![]() における接線の式は
における接線の式は
L (P,X) = 
南海 そう.これをそのまま係数を複素数まで認めることにして拡張すればよい.
ちなみに行列
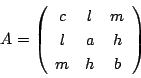
 を表す.
を表す.
二次曲線
![]() は適当な一次変換によって標準形になり,
それらは二次式による媒介変数表示をもつ.つまり二次曲線
は適当な一次変換によって標準形になり,
それらは二次式による媒介変数表示をもつ.つまり二次曲線![]() 上の点
上の点![]() は
は
次に二次行列
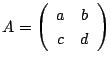 に対して
に対して![]() を行列式といい
を行列式といい
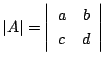 と表す.
と表す.
さらに三次行列
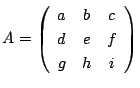 に対しその行列式
に対しその行列式![]() を
を
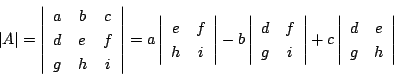
射影平面の2点
![]() と
と
![]() を通る直線の式は
を通る直線の式は

このとき直線![]() が
が![]() に接するための必要十分条件は,
に接するための必要十分条件は,
![]() のそれぞれに関する二次の等式で表される.
のそれぞれに関する二次の等式で表される.
証明
二次曲線![]() と
と![]() はそれぞれ行列
はそれぞれ行列![]() と
と![]() をもちいて
をもちいて
![]() はそれぞれ二次式によって
はそれぞれ二次式によって
![]() ,
,
![]() と表される.
と表される.
よって直線![]() は
は

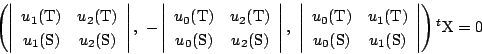
一方![]() 上の点
上の点![]() での接線は
での接線は
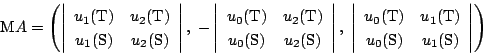
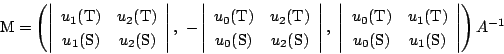
この![]() は
は![]() と
と![]() のそれぞれについて一次式である.
この
のそれぞれについて一次式である.
この![]() が
が![]() 上に存在することが,
上に存在することが,![]() が
が![]() に接することを意味する.
に接することを意味する.
この![]() を
を![]() の方程式
の方程式
![]() に代入すると,
確かに
に代入すると,
確かに
![]() のそれぞれに関する二次の等式になっている.□
のそれぞれに関する二次の等式になっている.□
この双二次式を
![]() と表す.
またこの式を
と表す.
またこの式を
![]() とも表す.
とも表す.
二つの二次曲線![]() と
と![]() がある.
がある.
![]() 上の点
上の点![]() から
から ![]() にひとつの接線をひき,
その延長が再び
にひとつの接線をひき,
その延長が再び ![]() と交わる点を
と交わる点を ![]() とする.
とする.
![]() から
から ![]() に
に
![]() とは異なる接線をひき,
その延長が再び
とは異なる接線をひき,
その延長が再び ![]() と交わる点を
と交わる点を ![]() とする.
このようにして点
とする.
このようにして点![]() を定める.
を定める.
点![]() が媒介変数
が媒介変数![]() で表され,
点
で表され,
点![]() が媒介変数
が媒介変数![]() で表されるとすると
で表されるとすると
![]() と
と![]() の間には,それぞれについて二次の関係式
の間には,それぞれについて二次の関係式
証明
数学的帰納法で示す.
![]() のとき.
のとき.
![]() なので成立する.
なので成立する.
![]() のとき.
のとき.
![]() として,連立方程式
として,連立方程式
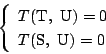
![]() は2個とれて,その各々から
は2個とれて,その各々から ![]() には
には
![]() ともう一つの接線が引ける.
よってこの関係式は
ともう一つの接線が引ける.
よってこの関係式は
![]() を重根にもつ.その二次関係式で約分される.
その式を
を重根にもつ.その二次関係式で約分される.
その式を
![]() とすれば.
とすれば.
![]() は
は![]() と
と![]() のそれぞれに関して二次式で,
のそれぞれに関して二次式で,
![]() の2根が
の2根が![]() を与える.
を与える.
![]() に対して
に対して
![]() が定まったとする.
連立方程式
が定まったとする.
連立方程式
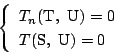
数学的帰納法によって証明が終わった.□
次に共役二次曲線を定義しよう.
![]() を二次曲線とし,その方程式を
を二次曲線とし,その方程式を
![]() とする.
とする.
![]() 上の点
上の点![]() に対し接線
に対し接線
![]() を定める.
この接線は
を定める.
この接線は
![]() が
が![]() 上を動くとき点
上を動くとき点
![]() で定まる軌跡を
で定まる軌跡を
![]() の共役二次曲線といい
の共役二次曲線といい![]() と表す.実際これは二次曲線になる.
と表す.実際これは二次曲線になる.
![]() と解いて
と解いて
![]() に代入すれば
に代入すれば
証明
ところが(1)から二次曲線![]() と
と![]() は交点を4つ持つので,
二次曲線
は交点を4つ持つので,
二次曲線![]() と
と![]() は4本の共有接線をもつ.□
は4本の共有接線をもつ.□
二つの二次曲線![]() と
と![]() がある.
がある.![]() とし,
とし,
![]() 上の点
上の点![]() から
から ![]() にひとつの接線をひき,
その延長が再び
にひとつの接線をひき,
その延長が再び ![]() と交わる点を
と交わる点を ![]() とする.
とする.
![]() から
から ![]() に
に
![]() とは異なる接線をひき,
その延長が再び
とは異なる接線をひき,
その延長が再び ![]() と交わる点を
と交わる点を ![]() とする.
このようにして点
とする.
このようにして点![]() を定める.
を定める.
![]() 上の点
上の点![]() で
で
![]() となるものが一つ存在すれば,
任意の
となるものが一つ存在すれば,
任意の![]() について
について
![]() となる.
となる.
証明
補題6によって
点![]() が媒介変数
が媒介変数![]() で表され,
点
で表され,
点![]() が媒介変数
が媒介変数![]() で表されるとすると
で表されるとすると
![]() と
と![]() の間には,それぞれについて二次の関係式
の間には,それぞれについて二次の関係式
点![]() が
が
![]() を満たすことは,
を満たすことは,![]() が
が
定理12 によって
![]() は四つの根を持つ.
は四つの根を持つ.
![]() より,
より,![]() は共通接線の接点ではない.
こうして
は共通接線の接点ではない.
こうして
![]() は,
さらに少なくとも一つ
は,
さらに少なくとも一つ![]() を定める
を定める![]() の値で成立するので,
この四次方程式は5個以上の根を持つ.したがって
の値で成立するので,
この四次方程式は5個以上の根を持つ.したがって
南海
入試問題からはじめて,まずそれを完全な形で解いた.
すると,虚数解をもつ四次方程式が現れる.
その正体を調べると,虚な共通接線を与える![]() の方程式だった.
の方程式だった.
入試問題を完全に解明しようとして,複素射影平面に至った. 高校数学や入試数学も学問として研究すれば,代数幾何学の入り口に来る,ということだ.