まずは次のトレミーの定理が必要だ.
定理 1 (トレミーの定理)
三角形 ![]() と点
と点 ![]() がある.このとき,
がある.このとき,
等号が成立するのは,
![]() が同一円周上にあるときである.
が同一円周上にあるときである.
拓生 トレミーの定理って, 不等式でしたか.
南海 いや.普通は同一円周上にあるとき等号が成立するところをいうのがトレミーの定理だ. 不等式の方は「オイラーの定理」というのだが,ここでは一般化されたトレミーの定理として, そのままトレミーの定理とする.
さてこれをどのように証明するかだ.
拓生 私の教科書の複素数の最後の「発展」に「トレミーの定理」の複素数を 使った証明が載っています.
南海 教科書の複素数を使う方法を少し発展させてやってみよう.
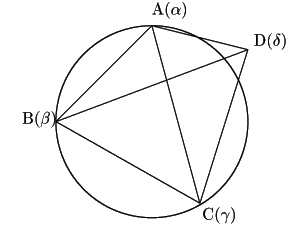 証明
証明
4点を表す複素数を順に,
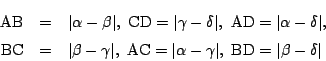
そこで,
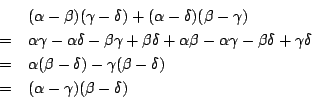
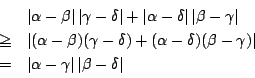
等号成立は負でない実数 ![]() で
で
変形すると,
南海 その通り.さていよいよ本題だが, 次の事実がなりたつのだよ.