しかし考えればこれはすべて平面![]() 上のことではないか.
いちいち円錐をかかなくても,平面幾何の問題として考えることはできないのか.
上のことではないか.
いちいち円錐をかかなくても,平面幾何の問題として考えることはできないのか.
小アジアの都市ベルガのアポロニウス(Apollonios,B.C.260〜200頃)は 平面曲線として楕円,双曲線,楕円を定義した.
耕一 それが,次の定義です.
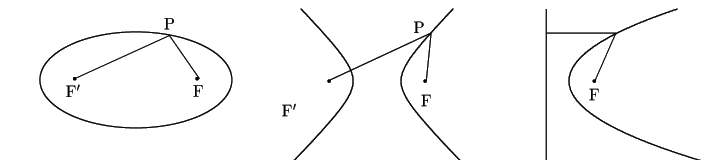
南海 実は,アポロニウスは放物線をこのようにはとらえなかった.
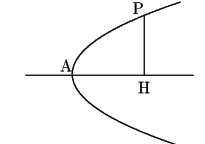 放物線上の点
放物線上の点![]() から放物線の軸に垂線
から放物線の軸に垂線![]() を引く.
また放物線の頂点を
を引く.
また放物線の頂点を![]() とする.
とする.
このとき
いずれにせよ,これで円錐曲線は平面上の曲線として考えればよいことがわかった.
アポロニウスはまた, 「ellipes(楕円)」,「parabola(放物線)」,「hyperbola(双曲線)」を命名した人である. ellipes,parabola,hyperbola はそれぞれ「不足する」,「一致する」,「過剰である」を意味する. このような呼び名はどこから来たのか.
楕円,双曲線では2つの焦点を結ぶ直線を軸といい, 放物線では焦点を通り準線に直交する直線を軸という.
曲線上の点![]() から軸に垂線
から軸に垂線![]() を引く.
軸と曲線の交点の一つを
を引く.
軸と曲線の交点の一つを![]() とする.
とする.
![]() ,
,![]() とおく.
とおく.
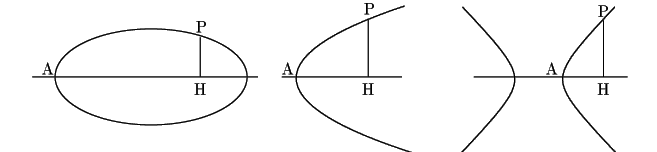
放物線のときは
![]() は一定であった.この比を
は一定であった.この比を![]() とすると
とすると
![]() と等号が成立する.これと同様にある定数
と等号が成立する.これと同様にある定数![]() を適当にとると
を適当にとると

アポロニウスは「円錐曲線」全8巻を後世に残した.これは16世紀までこの方面のまさに古典であった.
耕一 なるほど. 2点からの距離の比が一定な点の軌跡は円になるというアポロニウスの円もこの本にあるのですね.
南海 そうだ. しかしだ.アポロニウスの定義では,円錐曲線をそれぞればらばらにとらえていて, 何ら統一的な理解はできない. もともと円錐曲線は円錐を平面で切った切り口であるという統一的な把握からはじまったのに,である.
平面曲線としての統一的な把握はできないのか.放物線があまりにも他の二つとかけはなれている.
アポロニウスから500年後,エジプトのアレクサンドリアのパッポス(Pappos,A.D.390 頃)は 大著『数学集成』を編纂,そのなかでうまい定義を見いだしている. それは次のようなものである.
耕一 少し教科書にも載っています.
南海 これはおそらく次のような考察から得られたのではないかと思われる.
円錐を,切断平面![]() と直交し円錐の軸をとおる平面で切った断面
と直交し円錐の軸をとおる平面で切った断面![]() を考えよう.
を考えよう.
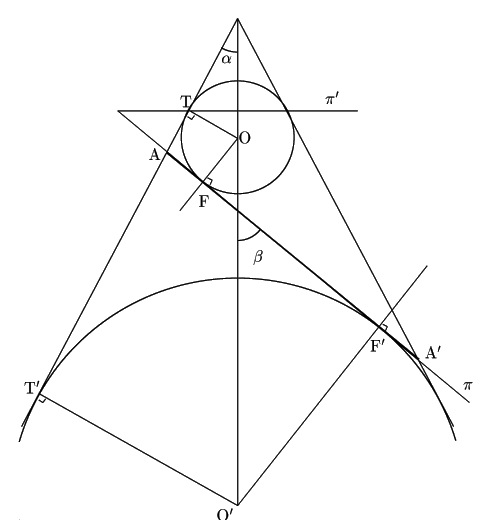 双曲線の場合も同じことなので楕円で考える.
双曲線の場合も同じことなので楕円で考える.
図の太線の部分が楕円を断面![]() に投影したものだ.
に投影したものだ.
![]() と円錐に接する2つの円の中心を
と円錐に接する2つの円の中心を
![]() とする.
とする.
2円と切断平面![]() との接点を
との接点を
![]() とする.
この2接点が楕円の焦点である.
とする.
この2接点が楕円の焦点である.
平面![]() 上の2円と円錐との接点をそれぞれ
上の2円と円錐との接点をそれぞれ
![]() とする.
平面
とする.
平面![]() 上の円錐と平面
上の円錐と平面![]() の交点をそれぞれ
の交点をそれぞれ
![]() とする.
とする.
もちろんこの記号は
ここでこれらの長さと角
![]() の間のどのような関係があるか.
の間のどのような関係があるか.
耕一
まず,
![]() を
を
![]() と関連づければよいのですね.
と関連づければよいのですね.
![]() からの2つの接線なので
からの2つの接線なので
また
南海
楕円であることはわかっているのだから
耕一
これから
すると
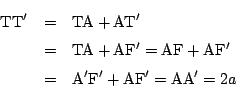
すると
となりました.
南海 パッポスはこのような考察から,逆に先述のような定義に至ったと思われる. いったんこの定義に至れば,それを座標平面において 座標平面上の問題として考えることもできる.
耕一 このような定義で円はどのように考えればよいのでしょうか.
南海
円は円錐を平面![]() で切断したという観点に立てば,
で切断したという観点に立てば,![]() が軸に直交している場合であり,
楕円の一種としてよい.
が軸に直交している場合であり,
楕円の一種としてよい.
ところが,準線で考えると,円錐では平面![]() と
と![]() が平行になり準線が存在しない.
この場合準線は無限のところに移行し,準線との距離が無限,
したがってその比としての離心率は0と考えなければならない.
楕円の極限として得られるともいえる.
この意味で退化した円錐曲線と考えてもよい.
が平行になり準線が存在しない.
この場合準線は無限のところに移行し,準線との距離が無限,
したがってその比としての離心率は0と考えなければならない.
楕円の極限として得られるともいえる.
この意味で退化した円錐曲線と考えてもよい.
切断平面![]() は頂点を通らないとしたが,
頂点を通るときは2直線か1直線か,1点になる.
この場合も,
は頂点を通らないとしたが,
頂点を通るときは2直線か1直線か,1点になる.
この場合も,![]() は頂点を通る位置に近づいた極限としてとらえることができ,
退化した円錐曲線と考えることができる.
は頂点を通る位置に近づいた極限としてとらえることができ,
退化した円錐曲線と考えることができる.