![]() 上の点
上の点![]() における
における![]() の接線は
『数学対話』−「パスカルの定理」で導いたところだが,もう一度確認してほしい.
の接線は
『数学対話』−「パスカルの定理」で導いたところだが,もう一度確認してほしい.
耕一
方程式(3)の両辺を![]() で微分すると
で微分すると
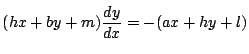 .したがって,点
.したがって,点
ここで,
![]() を用いて整理すると,
を用いて整理すると,
南海
したがってとくに
定理77 二次曲線 $ C $ と点P,および点Pその極線 $ l $ がある.
点Pを通る直線 $ m $と $ C $ との交点をA,B,
$ m $ と $ l $ の交点をQとする.このとき
\[
\dfrac{1}{\mathrm{AP}}+\dfrac{1}{\mathrm{BP}}=\dfrac{2}{\mathrm{PQ}}
\]
が成り立つ. ■
証明
点Pを原点, $ m $ を $ x $ 軸にとり,交点が $ x $ 軸の正の部分に来るように座標平面におく.
この結果点Qの座標は \[ \mathrm{Q}\left(-\dfrac{c}{f},\ 0 \right) \] である.次に,二次曲線$C$と$x$軸の交点の$x$座標は, 二次方程式 \[ ax^2+2fx+c=0 \] の二根である.点A,Bの$x$座標を$\alpha,\ \beta$とする. このとき \[ \alpha+\beta=-\dfrac{2f}{a} ,\ \alpha\beta=\dfrac{c}{a} \] となる.さて点P,Q,A,Bは同一直線上にあるので, $ x $ 座標に関して同様の関係が成り立つことを示せばよい. つまり \[ \dfrac{1}{\alpha}+\dfrac{1}{\beta}=\dfrac{2}{-\dfrac{c}{f}}=-\dfrac{2f}{c} \] ところが \[ \dfrac{1}{\alpha}+\dfrac{1}{\beta}=\dfrac{\alpha+\beta}{\alpha\beta} =-\dfrac{2f}{c} \] なので,成立している. □
耕一
これは円の場合などによく問題にありますが,このように一般的に成り立つのですね.
南海
この関係はすぐにわかるように
PA:AQ=PB:BQ
と同値である.これは,点A,BがPQを内分する比と外分する比が等しいことを意味し,この四点が調和点列をなすということ意味している.
このあたりが射影幾何での二次曲線の研究の始まりであった.またこの定理はより図形的な別の証明がある.これらについては『幾何学の精神』のなかの「諸定義とその関係」や「円錐曲線」を参考にしてほしい.
さてここで楕円,双曲線の基本性質. 証明法はいろいろある.最も基礎的な座標の方法で示そう.
証明
![]() の方程式を
の方程式を
![]() 上の点
上の点
![]() での接線
での接線![]() を
を
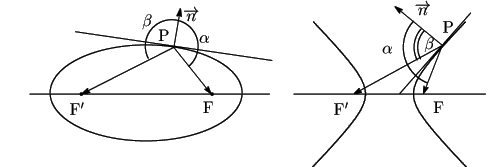
定理の証明を,
ベクトル
![]() がベクトル
がベクトル
![]() となす角
となす角![]() の余弦と,
ベクトル
の余弦と,
ベクトル
![]() がベクトル
がベクトル
![]() となす角
となす角![]() の余弦
を比較することでおこなう.
の余弦
を比較することでおこなう.
 楕円の場合
楕円の場合![]() を示せばよい.,
それはつまり
を示せばよい.,
それはつまり
双曲線の場合の場合
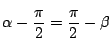 を示せばよい.,
それはつまり
を示せばよい.,
それはつまり
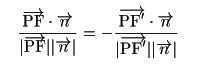

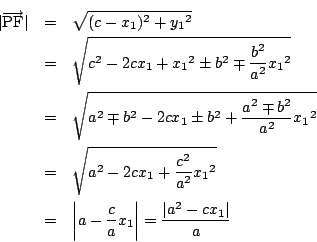
一方
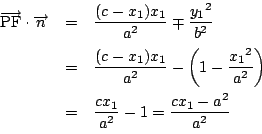
対称性から点![]() は第一象限にあるとしてよい.よって
は第一象限にあるとしてよい.よって
楕円の場合,![]() なので
なので
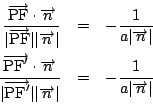
双曲線の場合,![]() なので
なので
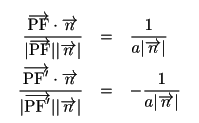
いずれの場合も証明すべきことが成立している.□
南海 定理(1)から,次のことがわかる.
同一平面上の楕円と双曲線の2つの焦点がそれぞれ一致しているとき, その楕円と双曲線は互いに直交している. ただし,楕円と双曲線が直交しているとは, 楕円と双曲線の各共有点におけるそれぞれの接線がその点で直交していることをいう.
耕一 図をかいてみますと,….
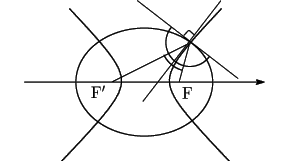 一目瞭然です.
一目瞭然です.
南海 直交性は直接示すこともできる.
耕一 やってみます.
![]() を
を![]() である正の定数として,楕円と双曲線の方程式を
である正の定数として,楕円と双曲線の方程式を
それぞれの焦点は
![]() と
と
![]() である.
焦点が一致するので
である.
焦点が一致するので
楕円と双曲線の共有点を![]() とする.
とする.![]() での接線の方程式は
での接線の方程式は
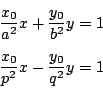
楕円と双曲線の共有点![]() なので
なので
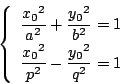
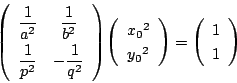
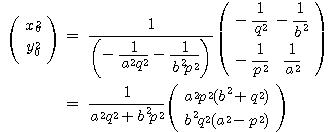
直交条件を調べる.

(5)から
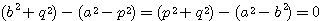
よって楕円と双曲線は互いに直交していることが示せた.□
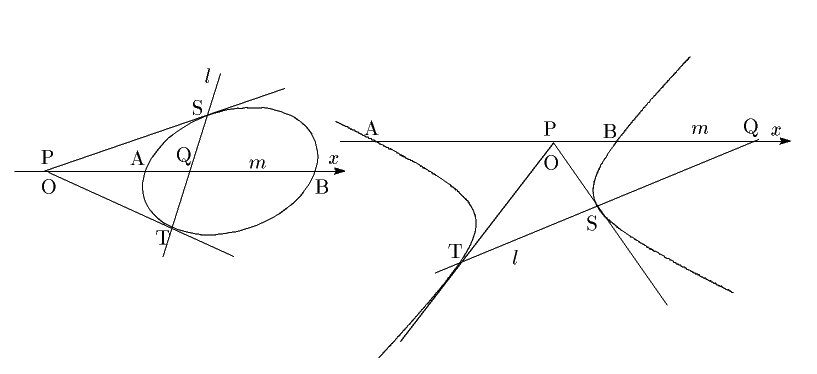
南海 定理(1)の楕円の部分は次のように図形的に示すことができる.
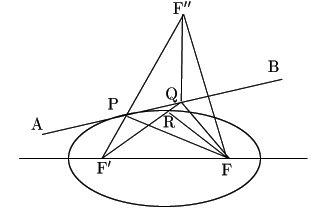 図のように接線
図のように接線![]() 上の動点
上の動点![]() をとる.
直線
をとる.
直線![]() と楕円の交点を
と楕円の交点を![]() とする.
すると楕円の定義と三角形の辺の不等式から
とする.
すると楕円の定義と三角形の辺の不等式から
つまり点![]() は点
は点![]() が接線上を動くとき
が接線上を動くとき
このような点の作図方法は?
耕一
接線に関して点![]() と対称な点を
と対称な点を![]() とする.
とする.
接線に関して点![]() と対称な点が
と対称な点が![]() なので
なので
南海 この図形的性質と,定理(1)とは独立に示された, 焦点共有な楕円と双曲線は直交するという事実から 定理(1)の双曲線の部分を導くことができる.
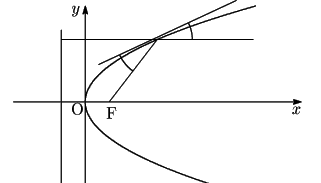 耕一
放物線の場合は,次の図のように接線が焦点となす角と,
接線が軸となす角が等しいのですね.
耕一
放物線の場合は,次の図のように接線が焦点となす角と,
接線が軸となす角が等しいのですね.
南海 その通りなのだ. が,前に離心率を考えたときと同様に, 放物線の場合は楕円や双曲線とは少し異なる方向に一般化される.
それが後で示す定理(2)だ.
この定理は上と同様に![]() 座標系の方程式から導くことができる.
ここではそれを極方程式を用いる方法で示そう.
座標系の方程式から導くことができる.
ここではそれを極方程式を用いる方法で示そう.