![]() 平面上の円
平面上の円![]() を
を
点![]() から円
から円![]() に直線
に直線![]() を引き,
その交点
を引き,
その交点![]() をとおり直線
をとおり直線![]() と直交する直線を
と直交する直線を
![]() とする.
とする.
![]() が円
が円![]() 上を動くとき,直線
上を動くとき,直線
![]() の通過する領域を求めてみよう.
の通過する領域を求めてみよう.
耕一
点![]() を
を
![]() とします.
とします.
角![]() がすべての値をとるとき,
点
がすべての値をとるとき,
点![]() が直線
が直線
![]() の通過する領域に存在することと,
方程式(6)をみたす
の通過する領域に存在することと,
方程式(6)をみたす![]() が存在することが同値です.
が存在することが同値です.
方程式(6)を![]() で整理すると
で整理すると
これをみたす![]() が存在する必要十分条件は
が存在する必要十分条件は
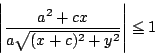
![]() つまり点
つまり点![]() が円
が円![]() の内部にあれば
の内部にあれば
![]() つまり点
つまり点![]() が円
が円![]() の外部にあれば
の外部にあれば

より双曲線の原点のある側です.その境界を図示します.

南海
この通過領域の境界がいわゆる直線
![]() の包絡線だ.
の包絡線だ.
包絡線は,方程式(6)を![]() で微分した式と式(6)を連立させて求めることもできる.
それは演習問題としよう.
で微分した式と式(6)を連立させて求めることもできる.
それは演習問題としよう.