

 次: 直辺四面体
上: 四面体の諸命題
前: 空間でのチャップル型定理
次: 直辺四面体
上: 四面体の諸命題
前: 空間でのチャップル型定理
南海
以下に述べることは,
故栗田稔先生の『初等数学15講』(1990年3月,自費出版)に教えられたことである.
補題 2
![$[\overrightarrow{a},\ \overrightarrow{b},\ \overrightarrow{c}]> 0$](images/img276.gif)
とする.また
とおく.このとき
であり.
が成り立つ.
■
証明
補題(1)より
したがって
同様に
ところが
![$[\overrightarrow{a},\ \overrightarrow{b},\ \overrightarrow{c}]> 0$](images/img276.gif) なので
なので
が成立する.□
この補題を用いると,空間図形のいろんな性質が簡明に示される.
いくつか例示する.
命題 2
4つの面の面積が等しい四面体(等積四面体)は,
各面が合同な四面体(等面四面体)である.
■
南海
これは『数学対話』−「等積四面体と等面四面体」で証明したことである.
その別証明を外積を用いておこなう.
証明
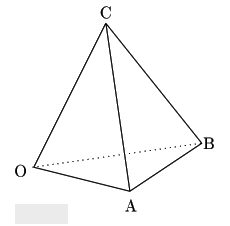 四面体
四面体 で
で
とし,
とおく.
さらに
とする.
このとき
つまり
である.
注意 1.1
これは一般の四面体で成立する.
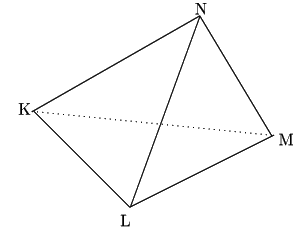 四面体
四面体 の4つの面の面積が
の4つの面の面積が
であるから,等積四面体では
が成り立つ.任意の点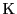 に対し
に対し
で点
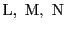 を定めると,
を定めると,
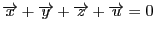 より
より
となる.
この四面体は4辺の長さが等しく正四面体である.
したがって4つの面の面積も等しい.
つまり
ここで補題(2)より
また
この結果
つまり
同様に
となり,四面体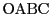 は等面四面体である.□
は等面四面体である.□


 次: 直辺四面体
上: 四面体の諸命題
前: 空間でのチャップル型定理
Aozora
2018-08-31
次: 直辺四面体
上: 四面体の諸命題
前: 空間でのチャップル型定理
Aozora
2018-08-31
![\begin{eqnarray*}
\overrightarrow{y}\times\overrightarrow{z}&=&
\overrightarro...
...a},\ \overrightarrow{b},\ \overrightarrow{c}]\overrightarrow{a}
\end{eqnarray*}](images/img280.gif)
![\begin{eqnarray*}
\vert\overrightarrow{x},\ \overrightarrow{y},\ \overrightarro...
...\overrightarrow{a},\ \overrightarrow{b},\ \overrightarrow{c}]^2
\end{eqnarray*}](images/img283.gif)
 四面体
四面体![]() で
で
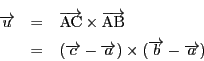
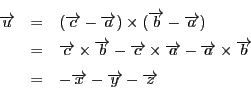
 四面体
四面体![\begin{eqnarray*}
\overrightarrow{x}\times\overrightarrow{u}&=&
\overrightarro...
...,\ \overrightarrow{c}]
(\overrightarrow{b}-\overrightarrow{c})
\end{eqnarray*}](images/img299.gif)