


次: 関連入試問題
上: 微分方程式とは
前: 微分方程式を解く
南海
簡単な場合に,条件を満たす微分方程式を立て,それを解くことが要求されうる.
曲線群をひとつの微分方程式で表すことが出来る.
例えば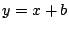 という形に書ける直線であることは,
という形に書ける直線であることは,
と表せる.また任意定数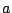 を用いて
を用いて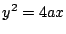 と表される放物線群は,
両辺を
と表される放物線群は,
両辺を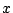 で微分し
で微分し
これから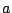 を消去して整理すると
を消去して整理すると
と書きあらわすことが出来る.
例 1.3
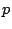
を任意の定数とし,放物線
を考える.
- すべての
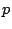 に対する
に対する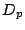 の方程式が満たす微分方程式を求めよ.
の方程式が満たす微分方程式を求めよ.
- すべての
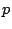 に対する
に対する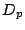 と直交し,かつ点
と直交し,かつ点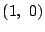 を通る曲線を求めよ.
を通る曲線を求めよ.
解答
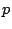 を任意の定数とし,放物線
を任意の定数とし,放物線
を考える.
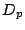 の方程式の両辺を
の方程式の両辺を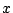 で微分する.
で微分する.
これから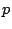 を消去して
を消去して
これが,すべての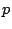 に対し
に対し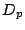 の方程式が満たす微分方程式である.
の方程式が満たす微分方程式である.
- すべての
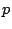 に対する
に対する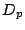 と直交する曲線の方程式は
と直交する曲線の方程式は
を満たさなければならない.これから
より
点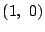 を通るので
を通るので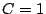 .
.
ゆえに曲線の方程式は
演習 3
解答
3
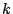
を0でない任意の定数とするとき,方程式
で表される曲線のすべてと直交する曲線の方程式を求めよ.
南海
また,量の相互関係を調べるときには,
現象のすべての量(変数)を確認し,それらの間の相互関係を書き出せばよい.
例 1.4
長さの単位を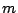 とする.
とする.
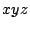 空間で,
空間で,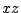 平面上の放物線
平面上の放物線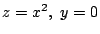 を
を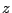 軸の周りに回転させた立体に,
毎秒
軸の周りに回転させた立体に,
毎秒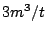 で水を入れる.水面の高さが
で水を入れる.水面の高さが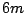 のときの水面の上昇速度を求めよ.
のときの水面の上昇速度を求めよ.
解答
ここに表れる量は体積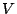 ,水面の高さ
,水面の高さ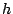 ,そして時間
,そして時間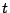 である.
それらの相互関係は
である.
それらの相互関係は
第2式から
第1式から
ここに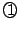 を代入して
を代入して
したがって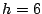 のとき水面の上昇速度
のとき水面の上昇速度
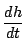 は
は
である.



次: 関連入試問題
上: 微分方程式とは
前: 微分方程式を解く
Aozora Gakuen
![]() という形に書ける直線であることは,
という形に書ける直線であることは,
![]() を任意の定数とし,放物線
を任意の定数とし,放物線
![]() を通るので
を通るので![]() .
.
![]() とする.
とする.
![]() 空間で,
空間で,![]() 平面上の放物線
平面上の放物線![]() を
を![]() 軸の周りに回転させた立体に,
毎秒
軸の周りに回転させた立体に,
毎秒![]() で水を入れる.水面の高さが
で水を入れる.水面の高さが![]() のときの水面の上昇速度を求めよ.
のときの水面の上昇速度を求めよ.![]() ,水面の高さ
,水面の高さ![]() ,そして時間
,そして時間![]() である.
それらの相互関係は
である.
それらの相互関係は