の,初期条件
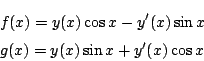
とおく.以下の問に答えよ.
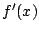 と
と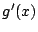 を求めよ.
を求めよ.
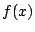 と
と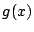 を求めよ.
を求めよ.
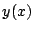 を求め,
を求め,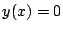 をみたす
をみたす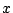 をすべて求めよ.
をすべて求めよ.
微分方程式
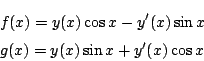
ある物体を地球の表面から鉛直上方に発射するとき,
発射してから![]() 秒後のこの物体と地球の中心との距離を
秒後のこの物体と地球の中心との距離を![]() mとすると,
微分方程式
mとすると,
微分方程式
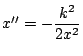 (
(![]() は正の定数) が成り立つ.
は正の定数) が成り立つ.
地球の半径を![]() m,初速を
m,初速を
![]() m/秒とするとき,
m/秒とするとき,
内側が直円すい形の容器がある.
その回転軸は鉛直で,頂点が最低点,深さは ![]() で,上面は半径
で,上面は半径 ![]() の円である.
この容器に上面まで満たされた水を,断面積が
の円である.
この容器に上面まで満たされた水を,断面積が ![]() の管を通じて.最低点からポンプで流出させるとする.
水の流出速度
の管を通じて.最低点からポンプで流出させるとする.
水の流出速度 ![]() は,そのときの水面の高さを
は,そのときの水面の高さを ![]() とすれば,
とすれば,
![]() (
(![]() は正の定数)で与えられるようにポンプが調整されているものとする.
流出し始めた時刻を
は正の定数)で与えられるようにポンプが調整されているものとする.
流出し始めた時刻を ![]() として,時刻
として,時刻 ![]() における水面の高さ
における水面の高さ ![]() を求めよ.
ただし,
を求めよ.
ただし,![]() は容器が空になる時刻までに限定する.
(時刻
は容器が空になる時刻までに限定する.
(時刻 ![]() と
と
![]() の間に流出する水量を
の間に流出する水量を
![]() とすれば,
とすれば,
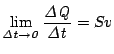 がなりたつ.)
がなりたつ.)
![]() は2次の導関数をもち,
は2次の導関数をもち, ![]() を満たす関数で,さらに次の性質をもつという.
原点を
を満たす関数で,さらに次の性質をもつという.
原点を ![]() とし,曲線
とし,曲線 ![]() 上の任意の点
上の任意の点
![]() に対し,
点
に対し,
点 ![]() を
を ![]() とするとき,
とするとき,
![]() の二等分線が曲線
の二等分線が曲線 ![]() の点
の点 ![]() における法線となる.
このとき,以下の問いに答えよ.
における法線となる.
このとき,以下の問いに答えよ.
深さ ![]() の容器がある.
底は半径
の容器がある.
底は半径 ![]() の円板,側面は
の円板,側面は
![]() のグラフを
のグラフを
![]() 軸の回りに回転したものである.
ただし
軸の回りに回転したものである.
ただし ![]() は正の連続関数で
は正の連続関数で ![]() とする.
この容器に単位時間あたり
とする.
この容器に単位時間あたり ![]() (一定)の割合で水を入れたとき,
(一定)の割合で水を入れたとき,
![]() 時間後に一杯になり,しかも
時間後に一杯になり,しかも ![]() 時間後の水面の面積は
時間後の水面の面積は ![]() であった.
であった.
関数 ![]() を決定し,
を決定し, ![]() を求めよ.
を求めよ.
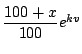 kg のガソリンを消費する車がある.
ここで
kg のガソリンを消費する車がある.
ここで