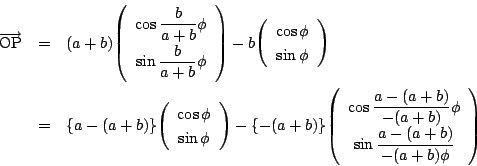南海
こういう曲線を外サイクロイドというのだが.
そういうときは半径![]() の円の周りを半径
の円の周りを半径![]() の円がまわるとして,
一般的な媒介変数表示を作ればよい.
の円がまわるとして,
一般的な媒介変数表示を作ればよい.
半径![]() の円を今後基準円,動く円を動円と呼ぶ.
の円を今後基準円,動く円を動円と呼ぶ.
 耕一
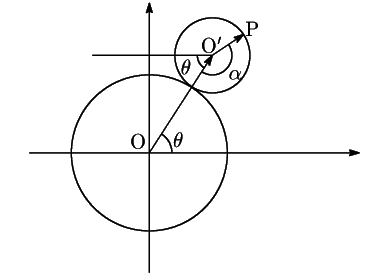
基準円の中心を
耕一
基準円の中心を![]() ,動円の中心を
,動円の中心を![]() とする.
とする.
図のように角![]() と
と![]() を反時計回りを正の方向にして定めると
を反時計回りを正の方向にして定めると
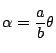 である.
ベクトル
である.
ベクトル
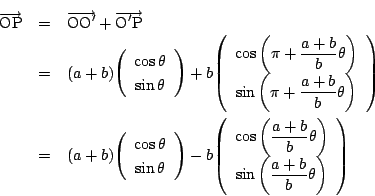
 です.
すると,先ほどの包絡線は
です.
すると,先ほどの包絡線は
光線が点![]() で曲線に接している様子がわかります.
で曲線に接している様子がわかります.
南海 もっと詳しくいろいろ調べることができるので,考えてほしい.
耕一 内側を回転してもいいのですね.
 南海
半径
南海
半径![]() の動円が半径
の動円が半径![]() の基準円の内側をまわるものだ.
記号の付け方を同様にすると,
方向も考えて
の基準円の内側をまわるものだ.
記号の付け方を同様にすると,
方向も考えて
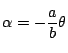 となる.
したがってベクトル
となる.
したがってベクトル
![]() が
が
![]() 軸の正の方向となす角は
軸の正の方向となす角は
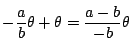 となり,
となり,
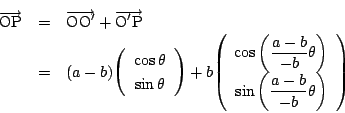
![]() ,b= なら図のような星形になる.
,b= なら図のような星形になる.
まとめると,円の周りを回転する円周上の定点の軌跡である外サイクロイドと内サイクロイドは,統一的に次のように媒介変数で表示されることになります.
![]() は正の数,
は正の数,![]() は0でない実数とします.
は0でない実数とします.
![]() が正なら半径
が正なら半径![]() の基準円に外接して半径
の基準円に外接して半径![]() の動円がまわるとき,
また
の動円がまわるとき,
また
![]() が負なら半径
が負なら半径![]() の基準円に内接して半径
の基準円に内接して半径![]() の動円がまわるとき,
その動円上の点
の動円がまわるとき,
その動円上の点![]() の軌跡の一般的な媒介変数表示は
の軌跡の一般的な媒介変数表示は
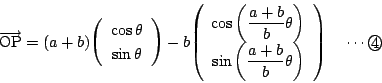
また![]() が負の時は,
が負の時は,
![]() の媒介変数表示が,
基準円の半径が
の媒介変数表示が,
基準円の半径が![]() のサイクロイドになるので,
のサイクロイドになるので,
![]() もまたサイクロイドになります.
もまたサイクロイドになります.
南海
それでよいのだが,内サイクロイドに関してすこし注意すべきことがある.
![]() のときは基準円と動円が一致する.これは除く. $ \dfrac{b}{a}\ne -1 $
としなければならない.
のときは基準円と動円が一致する.これは除く. $ \dfrac{b}{a}\ne -1 $
としなければならない.
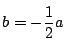 のときは,
のときは,
![]() となり,
動円上の点
となり,
動円上の点![]() の軌跡は基準円の直径そのものになる.
これは図を描いてもわかる.
これを退化した内サイクロイドといってもよい.このとき動点
の軌跡は基準円の直径そのものになる.
これは図を描いてもわかる.
これを退化した内サイクロイドといってもよい.このとき動点![]() は直線運動を行う.円運動が直線運動に変わる.これが遊星歯車の原理だ.例えば京都大学総合博物館にこのような模型がある.
その動きはまさに直線運動になる.
は直線運動を行う.円運動が直線運動に変わる.これが遊星歯車の原理だ.例えば京都大学総合博物館にこのような模型がある.
その動きはまさに直線運動になる.
![]() が負で
が負で![]() のときは
のときは![]() となる.
そこで
となる.
そこで![]() で
で
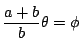 とおくと
とおくと