次： 特殊な函数を使うもの 上： 相加相乗平均の不等式の証明 前： 共通の設定

凸函数の性質を使うもの

まずはもっとも一般的な凸関数を使うものである． (2)の部分は98年大阪市立大学後期試験に出題されている．

方法 1
     関数 $f(x)$ が2回微分可能で$f''(x)<0$ を満たしているとする． また $n$ は$n\ge 2$ なる自然数とする．

1. $p+q=1$ を満たす任意の正の数$p,\ q$ と，関数の定義域の任意の$x,\ y$に対して，
   
   $$pf(x)+qf(y)\le f(px+qy)$$
   
   
   が成り立つことを平均値の定理を用いて示せ．

2. $p_1+p_2+ \cdots +p_n=1$ を満たす任意の正の数 $p_1，p_2， \cdots ，p_n$と， 定義域内の任意の実数 $x_1，x_2，\cdots ，x_n$ に対して
   
   $$p_1f(x_1)+p_2f(x_2)+ \cdots +p_nf(x_n)\le f(p_1x_1+p_2x_2+ \cdots +p_nx_n) \quad \cdots\maru{1}$$
   
   
   が成り立つことを示せ.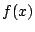
3. $f(x)$ として適切な関数を選ぶことにより
   
   $$G_n\le A_n$$
   
   
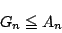
   を示し，等号が成立する場合を述べよ．

解

1. $x=y$ のときは等号が成立する．

   $x<y$ とする．このとき $x<px+qy<y$ である．

   区間 $[x,\ px+qy]$ で平均値の定理を用いると， $x<c_1<px+qy$ で
   

   $$f'(c_1)=\dfrac{f(px+qy)-f(x)}{(px+qy)-x}=\dfrac{f(px+qy)-f(x)}{q(y-x)}$$
   
   
   となるものが存在する． $p-1=-q$ を用いた．

   同様に区間 $[px+qy,\ y]$ で平均値の定理を用いると， $px+qy<c_2<y$ で
   

   $$f'(c_2)=\dfrac{f(y)-f(px+qy)}{y-(px+qy)}=\dfrac{f(y)-f(px+qy)}{p(y-x)}$$
   
   
   となるものが存在する． $1-q=p$ を用いた．

   $f''(x)<0$ で $c_1<c_2$ であるから $f'(c_1)>f'(c_2)$ ．つまり
   

   $$\dfrac{f(px+qy)-f(x)}{q(y-x)}>\dfrac{f(y)-f(px+qy)}{p(y-x)}$$
   
   
   これから
   
   $$pf(x)+qf(y)<f(px+qy)$$
   
   
   従って題意の不等式が成立し等号成立は $x=y$ のときである．
2. 数学的帰納法で示す．

   $n=2$ のときは(1)から成立．

   $n$個の場合に成立するとし $n+1$ 個の場合に成立することを示す．

   $q=p_1+p_2+\cdots+p_n$ とおく． $q+p_{k+1}=1$ であることに注意する．

   $$\begin{eqnarray*} &&p_1f(x_1)+p_2f(x_2)+ \cdots +p_nf(x_n)+p_{n+1}f(x_{n+1})\\ ... ...{n+1}\right)\\ &\le& f(p_1x_1+p_2x_2+ \cdots +p_{n+1}x_{n+1}) \end{eqnarray*}$$
   
   
   ゆえに $n+1$ の場合も成立した．等号成立は $x_1=\cdots=x_{n+1}$ のとき．

   よって一般の $n$ に対して題意が示された．

3. $f(x)=\log x$ とする． $f'(x)=\dfrac{1}{x},\ f''(x)=-\dfrac{1}{x^2}<0$ である．

   $p_1=p_2=\cdots=p_n=\dfrac{1}{n}$ で(2)の結果を用いる．
   

   $$\dfrac{\log a_1+\log a_2+\cdots+\log a_n}{n} \le \log \left(\dfrac{a_1+a_2+\cdots+a_n}{n} \right)$$
   
   
   
   
   $$∴ \quad \log (a_1a_2\cdots a_n)^{ \frac{1}{n}} \le \log \left(\dfrac{a_1+a_2+\cdots+a_n}{n} \right)$$
   
   
   つまり $G_n\le A_n$ が示された．等号成立は $a_1=\cdots=a_n$ のとき．□

方法 2 (1の別証)
     関数 $f(x)$ が2回微分可能で$f''(x)<0$ を満たしているとする． 定義域内の任意の$x,\ t$に対して

$$f(x)\le f'(t)(x-t)+f(t)$$

が成立することを示せ．

これを $x=x_1,\ x_2,\ \cdots,\ x_n$ および $$t=\sum_{k=1}^np_kx_k$$ で用いることにより1を示せ．

解

$$F(x)=f(x)-\{f'(t)(x-t)+f(t)\}$$

とおく．

$$F'(x)=f'(x)-f'(t),\ \quad F''(x)=f''(x)$$

$F'(t)=0$ で $F''(x)<0$ であるから $F(x)$ は $x=t$ で極大かつ最大である．

$F(t)=0$ であるから， 定義域内の任意の $x$ に対し$F(x)\le 0$ が成立する． 等号が成立するのは $x=t$ のときのみである．

つまり，定義域内の任意の$x,\ t$に対して

$$f(x)\le f'(t)(x-t)+f(t)$$

が成立することが示された．

$$t=\sum_{k=1}^np_kx_k$$として， $x$ に$x=x_k$ を代入し， $p_k$ をかけて $k=1,\ 2,\ \cdots,\ n$ について加える．

$$\begin{eqnarray*} \sum_{k=1}^n p_kf(x_k)&\le& \sum_{k=1}^n p_k\{f'(t)(x_k-t)+f(t... ...(t) \sum_{k=1}^n p_k\\ &=&f(t)=f\left(\sum_{k=1}^np_kx_k\right) \end{eqnarray*}$$

つまり1が示された．等号成立は各 $k$ に対する不等式で等号が成立するときであり， $x_k=t\ (\ k=1,\ 2\cdots,\ n\ )$ ，つまり $x_1=x_2=\cdots=x_n$ のときである．□

注 相加平均，相乗平均の不等式を導くだけなら，はじめから $p_k=\dfrac{1}{n}$ で 示せばよい．これは96年京都教育大学で出題されている．

この方法の優れているところは，数学的帰納法を使うことなく示せることである． 相加平均，相乗平均の不等式を導くために1の形まで示すのは，そうしないと 帰納法ができないからである．

次： 特殊な函数を使うもの 上： 相加相乗平均の不等式の証明 前： 共通の設定